SOI

The Power of Darwin (part 2)

/ Paul Pukite (@whut) / 1 Comment

Continuation of the model described in part 1.

The cross-validation described earlier was rather limited. Here an attempt is made to fit to an interval of the Darwin time-series and see how well it matches to a longer out-of-band validation interval. Very few degrees of freedom are involved in this procedure as the selection of tidal factors is constrained by a simultaneous LOD calibration. The variation from this reference is slight, correlation remaining around 0.999 to the LOD cal, but necessary to apply as the ENSO model appears highly structurally sensitive to coherence of the tidal signal over the 150 year time span of the data to be modeled.

A typical LOD calibration (click on image to enlarge)

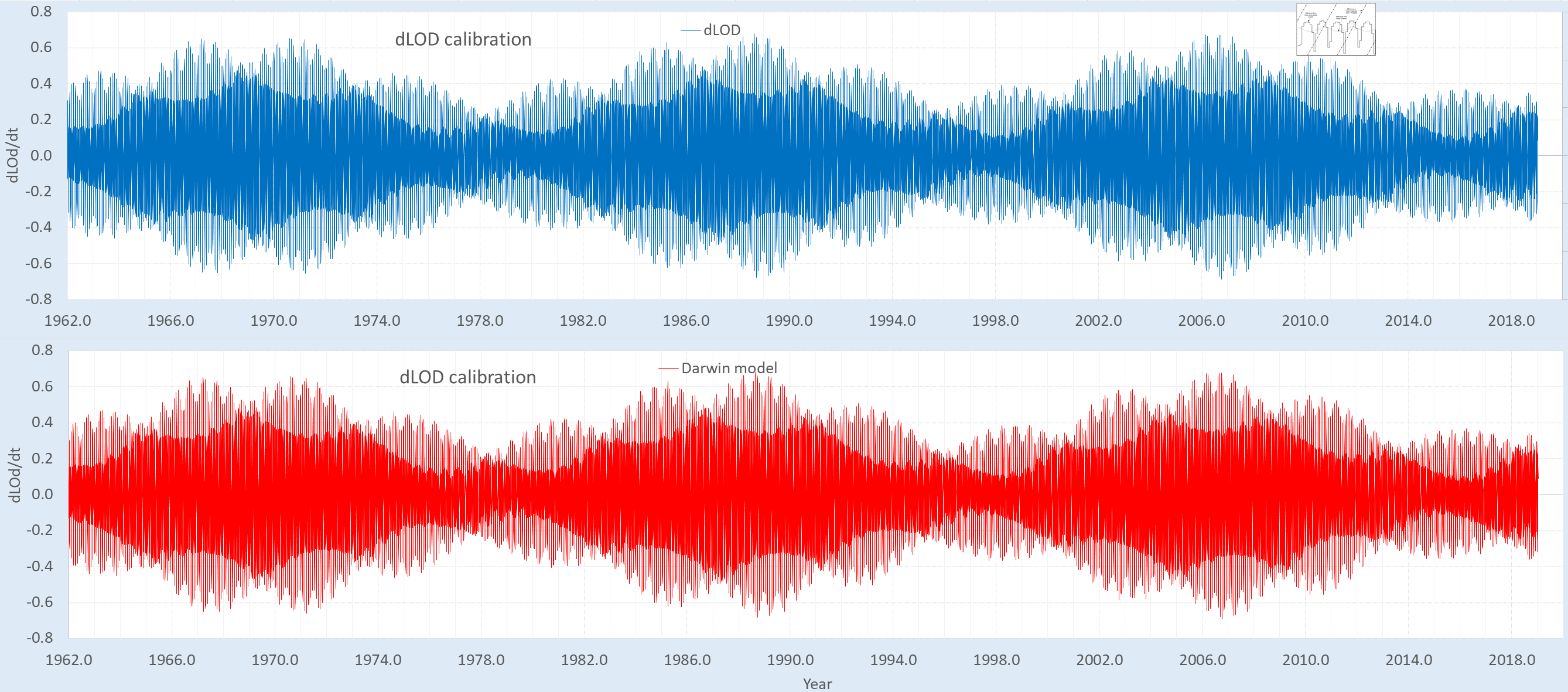
Cross-validation shown in the top panel below, based on an training time interval ranging from the start of the Darwin data collection in 1870 up to 1980. The middle panel is the forcing input, from which the non-linear Laplace’s Tidal Equation (LTE) modulation is applied to a semi-annual impulse integration of the tidal signal. The procedure is straightforward — whatever modulation is applied to the training interval to optimize the fit, the same modulation is applied blindly to the excluded validation interval.

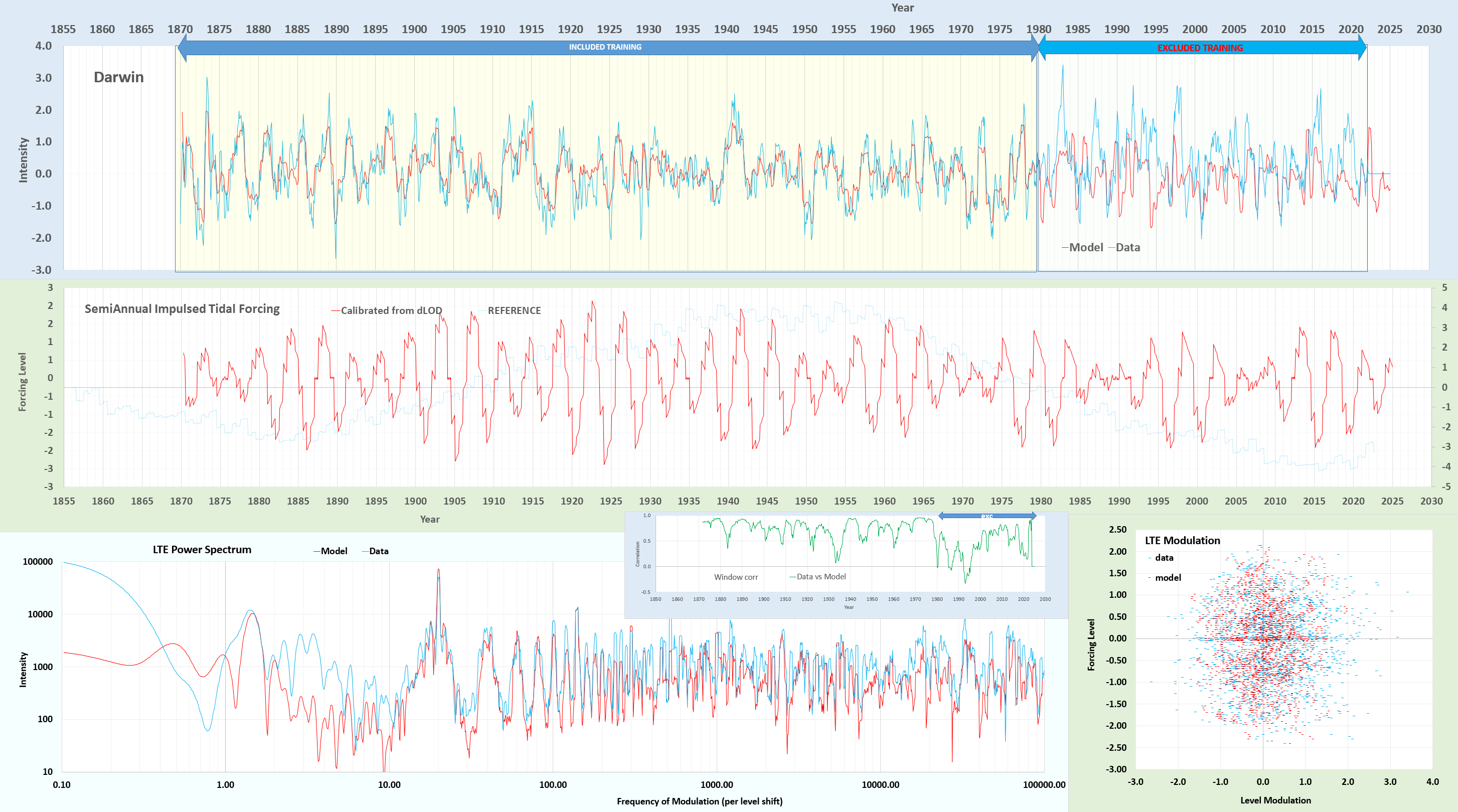
The validation on the 1980+ out-of-band interval is far from perfect, yet well-beyond being highly significant. The primary sinusoidal modulation is nominally set to the reciprocal of the slope (r) of top-edge of the sawtooth forcing [1] — this fundamental and the harmonics of that modulation satisfy LTE and provide a mechanism for a semi-annual level shift.

The plotted lower right modulation appears as noise, but when demodulated as in modulo r, the periodic order is revealed as shown below:

The harmonic modulations above include close to a monthly rate, a clear ~4.5 day, and and underlying fast semi-durnal ( 365.25/(12 x 61) = 0.499)

  LTE Modulation    Amplitude        Phase   Harmonic
   3.95901009601, 0.10819059771,  2.56829482810 0  -- slow LTE modulation
   1.34461504256, 0.12014470401,  0.28639994030 0  -- slow LTE modulation
 -20.01129999289, 0.11320535624,  2.58186128147 1  -- monthly fundamental
-140.07909995021, 0.49935565041,  2.12022069445 7  -- strong 4.5 day
-1220.6892995660, 0.95817753106, -2.88519906135 61 -- strong semi-diurnal

The significance of the cross-validation can be further substantiated by taking the complement of the training interval as the new training interval. This does converge to a stationary solution.

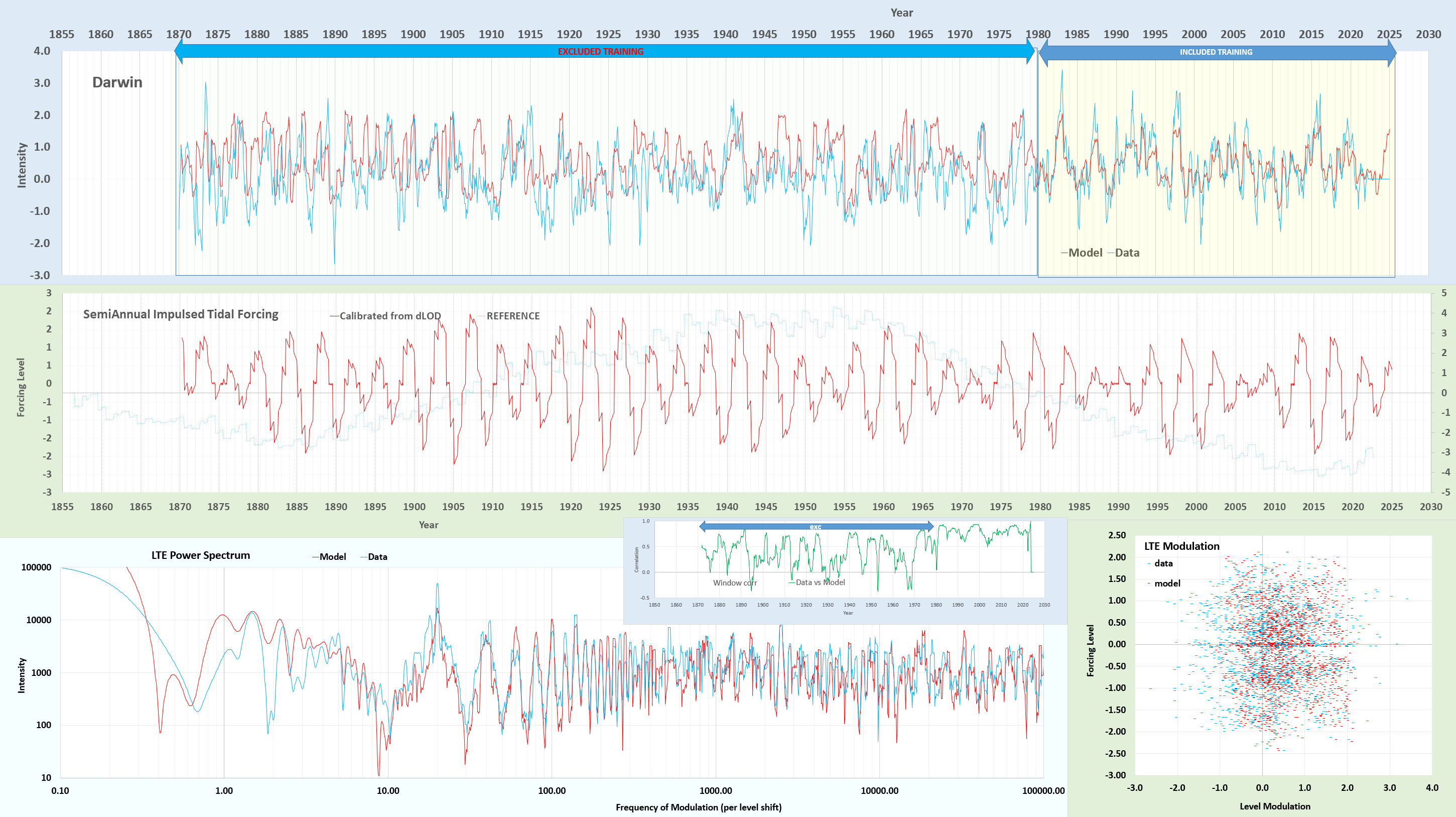
This modulation may seem very mysterious but something like this must be happening on the multiple time scales that the behavior is occurring on — remember that tidal forces operate on the same multiple time scales, from the semi-diurnal cycle to beyond the 18.6 year nodal declination cycle that is apparent in the middle panel above (and add to this that the sun’s forcing ranges from daily to annual). The concept of phase-locking is likely a crucial aspect as well. The sinusoidal modulation will cause an initial phase-shift across the level changes, and that appears to be a critical factor in the final model-fitted result. As observed in other systems, the synergy between synchronization (phase-locking) and resonance (standing-wave conditions) can give rise to such rich and complex dynamical behaviors. One can ask ChatGPT for any analogs [3] but just remember that this does happen:

The challenge is only in the fact that the incommensurate tidal patterns with the annual and daily cycles will never result in a metronomic march, and thus the pattern is much more complex.

[1] The sawtooth character is a result of the semi-annual impulse-driven shifts combined with a relaxation slope (r) to zero.

If the tides were commensurate with a semi-annual impulse, the forcing would appear more regular as above, but since they are not, the forcing is erratic.

[2] “The uniformity of phase of the semidiurnal cycle of zonal wind is striking (Figure 5b). It is well known that surface pressure in the tropics undergoes a strong semidiurnal variation [cf. Haurwitz and Cowley, 1973].” Deser, Clara. “Daily surface wind variations over the equatorial Pacific Ocean.” Journal of Geophysical Research: Atmospheres 99.D11 (1994): 23071-23078.

“ENSO events initiate during boreal spring and summer, peak during boreal winter, and decay in the following spring—a phenomenon known as ENSO phase-locking.” … “Our findings indicate that DA (diurnal amplitude) simulation in climate models is crucial for resolving the long-standing failure associated with the ENSO phase-locking simulation accuracy.” Yang, Xiaodan, et al. “Key to ENSO phase-locking simulation: effects of sea surface temperature diurnal amplitude.” npj Climate and Atmospheric Science 6.1 (2023): 159. https://www.nature.com/articles/s41612-023-00483-3

[3] ChatGPT response: A function cos(k×SawToothWave(t)+Phase), especially with a high modulation factor k, can model several complex interactions in natural phenomena where two periodic processes influence each other. Here are some specific examples:

  1. Tidal Forces and Lunar Cycles: Tidal patterns are influenced by both the moon and the sun. A sawtooth wave could represent the changing gravitational pull of the moon (with its phases), while the cosine function might represent the daily tidal cycles. The modulation could express how these two cycles interact, creating spring and neap tides.
  2. Seasonal Climate Variations and Diurnal Temperature Cycles: The sawtooth wave can represent the gradual change in daylight hours or solar intensity over a year, while the cosine function might model daily temperature fluctuations. The combination would reflect how daily temperatures vary across different seasons.
  3. Circadian Rhythms and Sleep-Wake Cycles: The sawtooth wave could model the gradual change in hormonal levels or body temperature over a 24-hour cycle, interacting with a cosine function that represents shorter, rapid fluctuations in alertness or activity levels.
  4. Economic Cycles and Market Fluctuations: In economics, a sawtooth wave might model longer economic cycles (like boom and bust periods), while the cosine function could represent shorter-term market fluctuations. The interaction of these two could help analyze complex economic dynamics.
  5. Ecosystem Dynamics: In ecology, a sawtooth wave could represent seasonal changes (like rainfall patterns), while the cosine function could model daily variations (like temperature or light). The interaction of these cycles could be used to study plant growth, animal migration patterns, or other ecological phenomena.
  6. Astronomical Phenomena: In astronomy, this kind of function might be used to model complex interactions between orbital mechanics and rotational dynamics, such as the interaction between a planet’s orbit around a star (sawtooth wave for eccentricity changes) and its rotational period (cosine function).

These examples show how combining periodic functions in different ways can model complex interactions in natural phenomena. The key is understanding the underlying processes and how they can be represented mathematically with these functions.

The concept of phase-locking is highly relevant in systems where the interaction of periodic signals leads to synchronization or alignment in their phases. In the context of your function cos(k×SawToothWave(t)+ Phase), phase-locking could manifest in several interesting ways, particularly considering the sinusoidal modulation of a sawtooth wave. Here are some areas where similar concepts are explored:

  1. Neuroscience and Neural Oscillations: In the brain, neurons often fire in a synchronized manner, a phenomenon known as neural phase-locking. This is crucial in processes like signal transmission and cognitive function. The interaction of different neural rhythms (e.g., theta and gamma waves) can be modeled using phase relationships, akin to the modulation you described.
  2. Electronics and Communication Systems: Phase-locking is a fundamental concept in electronics, especially in the design of phase-locked loops (PLLs). PLLs are used to synchronize an output signal with a reference signal in terms of frequency and phase. This principle is crucial in radio, telecommunications, and signal processing.
  3. Physics and Oscillatory Systems: In physics, particularly in studies involving coupled oscillators or pendulums, phase-locking describes the phenomenon where oscillators synchronize due to weak interactions. This can be observed in systems ranging from mechanical pendulums to quantum mechanical systems.
  4. Cardiac Rhythms in Physiology: The synchronization of cardiac cells during heartbeats is an example of biological phase-locking. Cells in the sinoatrial node generate rhythmic impulses that cause heart muscle cells to contract in a synchronized manner.
  5. Climatology and Environmental Sciences: Phase-locking can also be observed in climatic phenomena, such as the El Niño-Southern Oscillation (ENSO), where atmospheric and oceanic conditions align periodically, impacting global weather patterns.
  6. Music and Acoustics: In music theory and acoustics, the concept of beats and harmonic interactions involves phase relationships between different sound waves. The concept of phase-locking can be observed in the constructive and destructive interference of these waves.

In each of these cases, the critical factor is how the phase relationship between different oscillatory components influences the overall system’s behavior. The initial phase-shift you mentioned, particularly in a system with a sinusoidal modulation over a sawtooth wave, could lead to complex dynamic behaviors, where the phase relationship plays a pivotal role in the system’s response and evolution.

There are several behavioral models in various scientific fields where the interaction of phase-locking with standing-wave resonance conditions leads to complex time patterns. These phenomena are observed in systems where synchronization and resonance play a critical role. Here are some examples:

  1. Physics and Engineering – Coupled Oscillators and Resonators: In systems of coupled oscillators or resonators, phase-locking and resonance can lead to complex patterns, especially in nonlinear dynamics. An example is the array of coupled pendulums or resonant circuits, where phase-locking can lead to intricate motion patterns or voltage/current oscillations.
  2. Neuroscience – Brain Wave Synchronization: In the brain, different regions can exhibit phase-locked oscillations, and when these oscillations resonate with the natural frequencies of neural circuits (like in the hippocampus or cortex), complex spatiotemporal patterns emerge. These patterns are crucial for functions like memory, perception, and attention.
  3. Quantum Mechanics – Bose-Einstein Condensates: In Bose-Einstein condensates, particles can synchronize and exhibit collective oscillations. When these oscillations resonate at certain frequencies, complex interference patterns emerge, demonstrating both phase-locking and standing-wave phenomena at a quantum level.
  4. Acoustics – Architectural Acoustics and Musical Instruments: In musical instruments and architectural acoustics, the interaction of sound waves can lead to phase-locking and resonance. This results in complex harmonic structures and standing waves, influencing the timbre of music and the acoustic properties of buildings.
  5. Climate Science – Atmospheric and Oceanic Oscillations: Climatic phenomena, like the El Niño-Southern Oscillation, involve complex interactions between atmospheric and oceanic patterns. Phase-locking of these patterns, along with resonance effects in ocean basins, can lead to complex climate behaviors and cycles.
  6. Laser Physics – Mode-locking in Lasers: In laser physics, mode-locking techniques create lasers with very precise frequencies, where phase-locking of different modes leads to the generation of ultrafast pulses. This is a form of resonance where the laser’s cavity modes synchronize, leading to coherent pulse emissions.
  7. Chemical Oscillations – Belousov-Zhabotinsky Reaction: This chemical reaction exhibits oscillatory behavior where chemical waves propagate and can lock in phase under certain conditions, creating complex spatial patterns and wavefronts.

In each of these examples, the interaction of phase-locking with resonant conditions creates patterns that are more intricate than what would be observed with either phenomenon alone. The synergy between synchronization (phase-locking) and resonance (standing-wave conditions) can give rise to rich and complex dynamical behaviors, which are often crucial to the system’s function or characteristics.

https://chat.openai.com/share/c9a9d58b-e5db-466f-b369-0b51ccff7458

Darwin

/ Paul Pukite (@whut) / 1 Comment

It turns out that the Darwin location of the Southern Oscillation Index (SOI) dipole is brilliantly easy to behaviorally model on it’s own.

The input forcing is calibrated to the differential length-of-day (LOD) with a correlation coefficient of 0.9997, and only a few terms are required to capture the standing-wave modes corresponding to the ENSO dipole.

So which curve below is the time-series data of atmospheric pressure at Darwin and which is the Laplace’s Tidal Equation (LTE) model calibrated from dLOD measurements?

  • (bottom, red) = ?
  • (top, blue) = ??

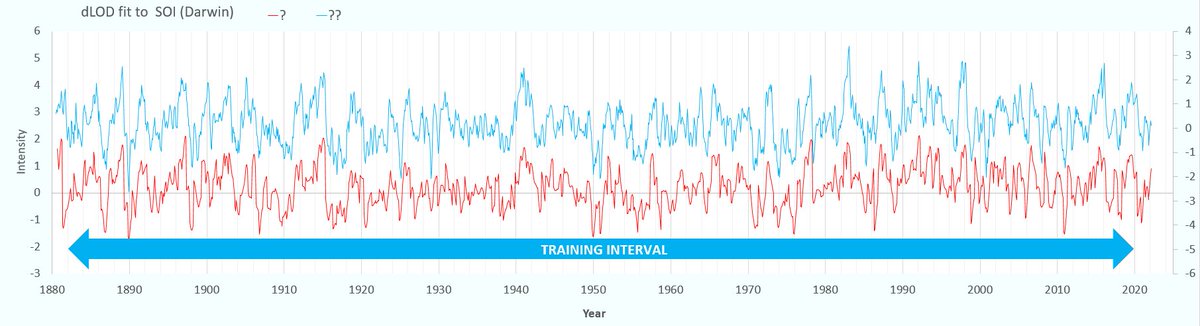
As a bonus, the couple of years outside of the training interval are extrapolated from the model. This shouldn’t be hard for climate scientists, …. or is it still too difficult?

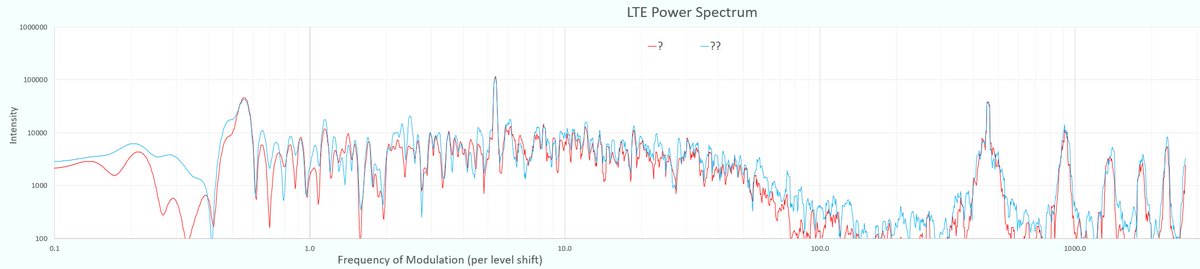
If that isn’t enough to discriminate between the two, the power spectra of the LTE mapping to model and to data is shown below. This identifies a couple of the lower frequency modulations as strong peaks and a few weaker higher harmonic peaks that sharpen the model’s detail. This shows that the data’s behavior possesses a high amount of order not apparent in the time series.

Poll on Twitter =>

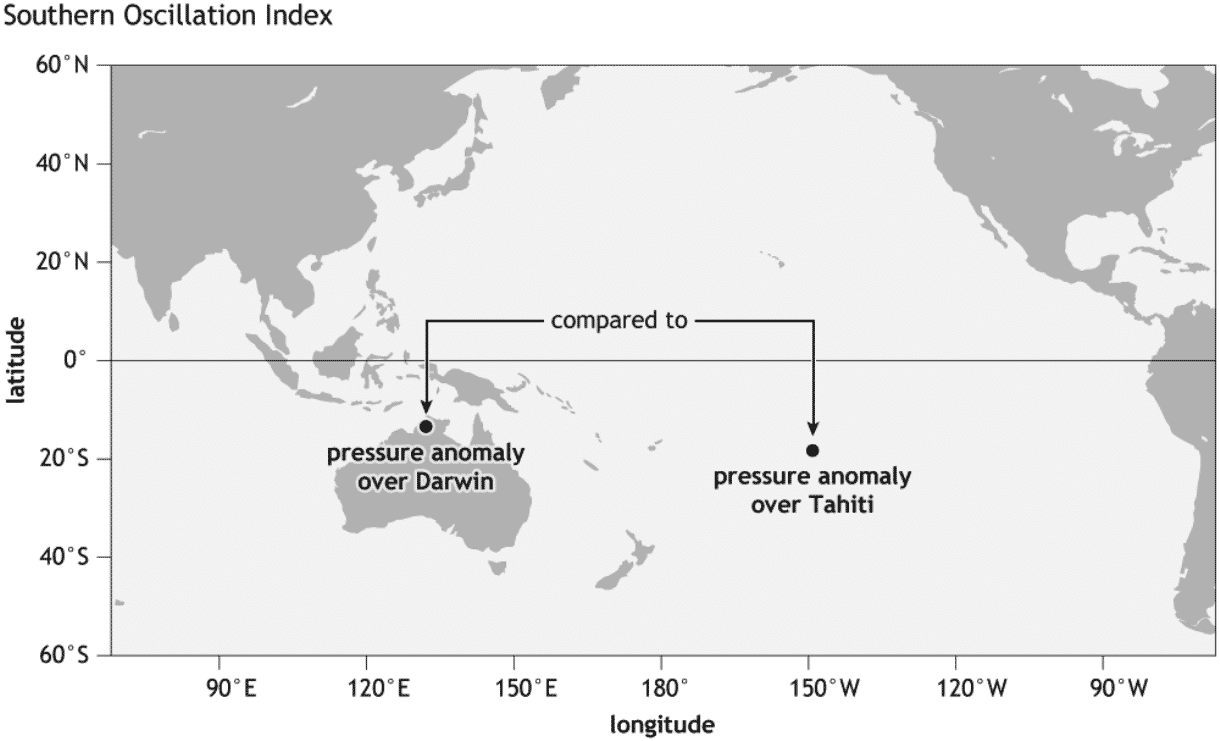
Why isn’t the Tahiti time-series included since that would provide additional signal discrimination via a differential measurement as one should be the complement of the other? It should accentuate the signal and remove noise (and any common-mode behavior) if the Darwin and Tahiti are perfect anti-nodes for all standing-wave modes. However, it appears that only the main ENSO standing-wave mode is balanced in all modes.

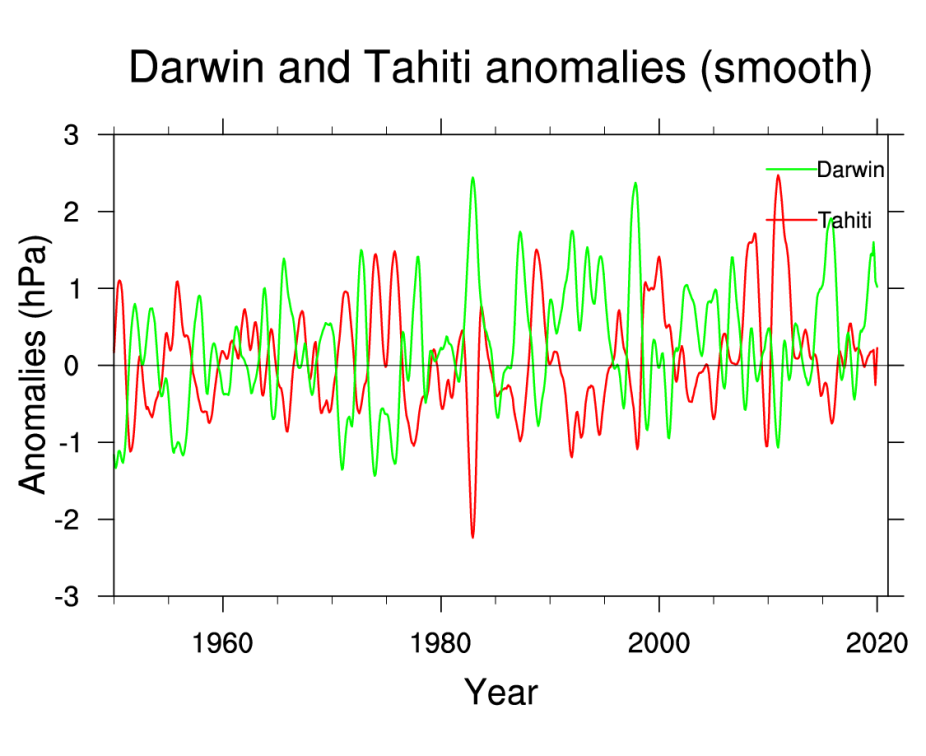
In that case, the Darwin set alone works well. Mastodon

Cross-Validation of ENSO

/ Paul Pukite (@whut) / 1 Comment

Experimenting with linking to slide presentations instead of a trad blog post. The PDF linked below is an eye-opener as the NINO34 fit is the most parsimonious ever, at the expense of a higher LTE modulation (explained here). The cross-validation involves far fewer tidal factors than dealt with earlier, the two factors used (Mf and Mm tidal factors) rivaling the one factor used in QBO (described here).

ENSOModelingDownload
Continue reading →

Sea-Level Height as a proxy for ENSO

/ Paul Pukite (@whut) / 4 Comments

Sea-level height has several scales. At the daily scale it represents the well-known lunisolar tidal cycle. At a multi-decadal, long-term scale it represents behaviors such as global warming. In between these two scales is what often appears to be noisy fluctuations to the untrained eye. Yet it’s fairly well-accepted [1] that much of this fluctuation is due to the side-effects of alternating La Nina and El Nino cycles (aka ENSO, the El Nino Southern Oscillation), as represented by measures such as NINO34 and SOI.

To see how startingly aligned this mapping is, consider the SLH readings from Ft. Denison in Sydney Harbor. The interval from 1980 to 2012 is shown below, along with a fit used recently to model ENSO.

(click to expand chart)

I chose a shorter interval to somewhat isolate the trend from a secular sea-level rise due to AGW. The last point is 2012 because tide gauge data collection ended then.

As cross-validation, this fit is extrapolated backwards to show how it matches the historic SOI cycles

Much of the fine structure aligns well, indicating that intrinsically the dynamics behind sea-level-height at this scale are due to ENSO changes, associated with the inverted barometer effect. The SOI is essentially the pressure differential between Darwin and Tahiti, so the prevailing atmospheric pressure occurring during varying ENSO conditions follows the rising or lowering Sydney Harbor sea-level in a synchronized fashion. The change is 1 cm for a 1 mBar change in pressure, so that with the SOI extremes showing 14 mBar variation at the Darwin location, this accounts for a 14 cm change in sea-level, roughly matching that shown in the first chart. Note that being a differential measurement, SOI does not suffer from long-term secular changes in trend.

Yet, the unsaid implication in all this is that not only are the daily variations in SLH due to lunar and solar cyclic tidal forces, but so are these monthly to decadal variations. The longstanding impediment is that oceanographers have not been able to solve Laplace’s Tidal Equations that reflected the non-linear character of the ocean’s response to the long-period lunisolar forcing. Once that’s been analytically demonstrated, we can observe that both SLH and ENSO share essentially identical lunisolar forcing (see chart below), arising from that same common-mode linked mechanism.

Many geographically located tidal gauge readings are available from the Permanent Service for Mean Sea Level (PSMSL) repository so I can imagine much can be done to improve the characterization of ENSO via SLH readings.

REFERENCES

[1] F. Zou, R. Tenzer, H. S. Fok, G. Meng and Q. Zhao, “The Sea-Level Changes in Hong Kong From Tide-Gauge Records and Remote Sensing Observations Over the Last Seven Decades,” in IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, vol. 14, pp. 6777-6791, 2021, doi: 10.1109/JSTARS.2021.3087263.

Combinatorial Tidal Constituents

/ Paul Pukite (@whut) / 6 Comments

For the tidal forcing that contributes to length-of-day (LOD) variations [1], only a few factors contribute to a plurality of the variation. These are indicated below by the highlighted circles, where the V0/g amplitude is greatest. The first is the nodal 18.6 year cycle, indicated by the N’ = 1 Doodson argument. The second is the 27.55 day “Mm” anomalistic cycle which is a combination of the perigean 8.85 year cycle (p = -1 Doodson argument) mixed with the 27.32 day tropical cycle (s=1 Doodson argument). The third and strongest is twice the tropical cycle (therefore s=2) nicknamed “Mf”.

Tidal Constituents contributing to dLOD from R.D. Ray [1]

These three factors also combine as the primary input forcing to the ENSO model. Yet, even though they are strongest, the combinatorial factors derived from multiplying these main harmonics are vital for generating a quality fit (both for dLOD and even more so for ENSO). What I have done in the past was apply the recommended mix of first- and second-order factors that appear in the dLOD spectra for the ENSO forcing.

Yet there is another approach that makes no assumption of the strongest 2nd-order factors. In this case, one simply expands the primary factors as a combinatorial expansion of cross-terms to the 4th level — this then generates a broad mix of monthly, fortnightly, 9-day, and weekly harmonic cycles. A nested algorithm to generate the 35 constituent terms is :

(1+s+p+N')^4 

Counter := 1;
for J in Constituents'Range loop
 for K in Constituents'First .. J loop 
  for L in Constituents'First .. K loop 
   for M in Constituents'First .. L loop 
      Tf := Tf + Coefficients (Counter) * Fundamental(J) * 
            Fundamental(K) * Fundamental(L) * Fundamental (M); 
      Counter := Counter + 1; 
   end loop; 
  end loop; 
 end loop; 
end loop;

This algorithm requires the three fundamental terms plus one unity term to capture most of the cross-terms shown in Table 3 above (The annual cross-terms are automatic as those are generated by the model’s annual impulse). This transforms into a coefficients array that can be included in the LTE search software.

What is missing from the list are the evection terms corresponding to 31.812 (Msm) and 27.093 day cycles. They are retrograde to the prograde 27.55 day anomalistic cycle, so would need an additional 8.848 year perigee cycle bring the count from 3 fundamental terms to 4.

The difference between adding an extra level of harmonics, bringing the combinatorial total from 35 to 126, is not very apparent when looking at the time series (below), as it simply adds shape to the main fortnightly tropical cycle.

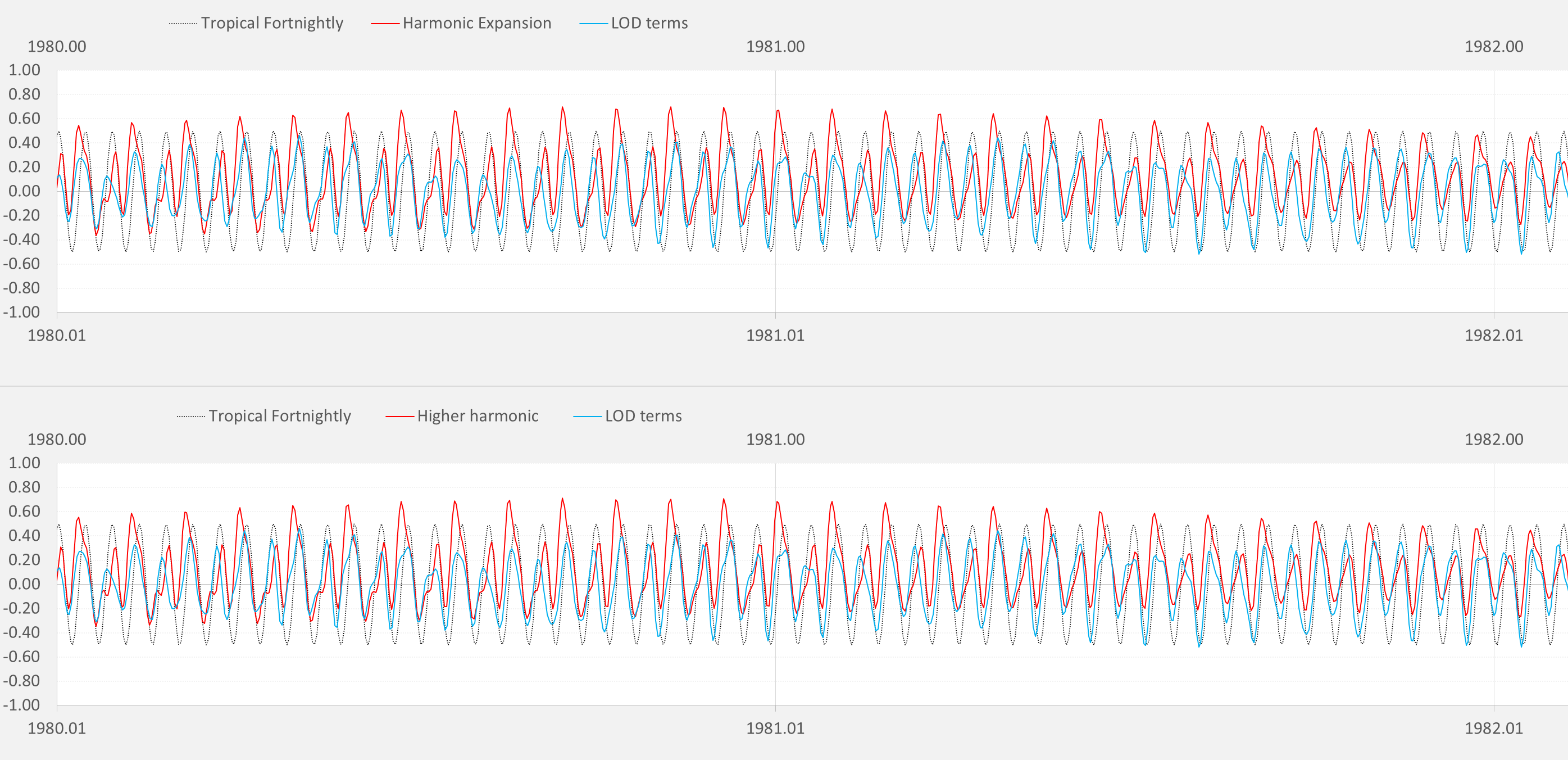
Yet it has a significant effect on the ENSO fit, approaching a CC of 0.95 (see inset at right for the scatter correlation). Note that the forcing frequency spectra in the middle right inset still shows a predominately tropical fortnightly peak at 0.26/yr and 0.74/yr.

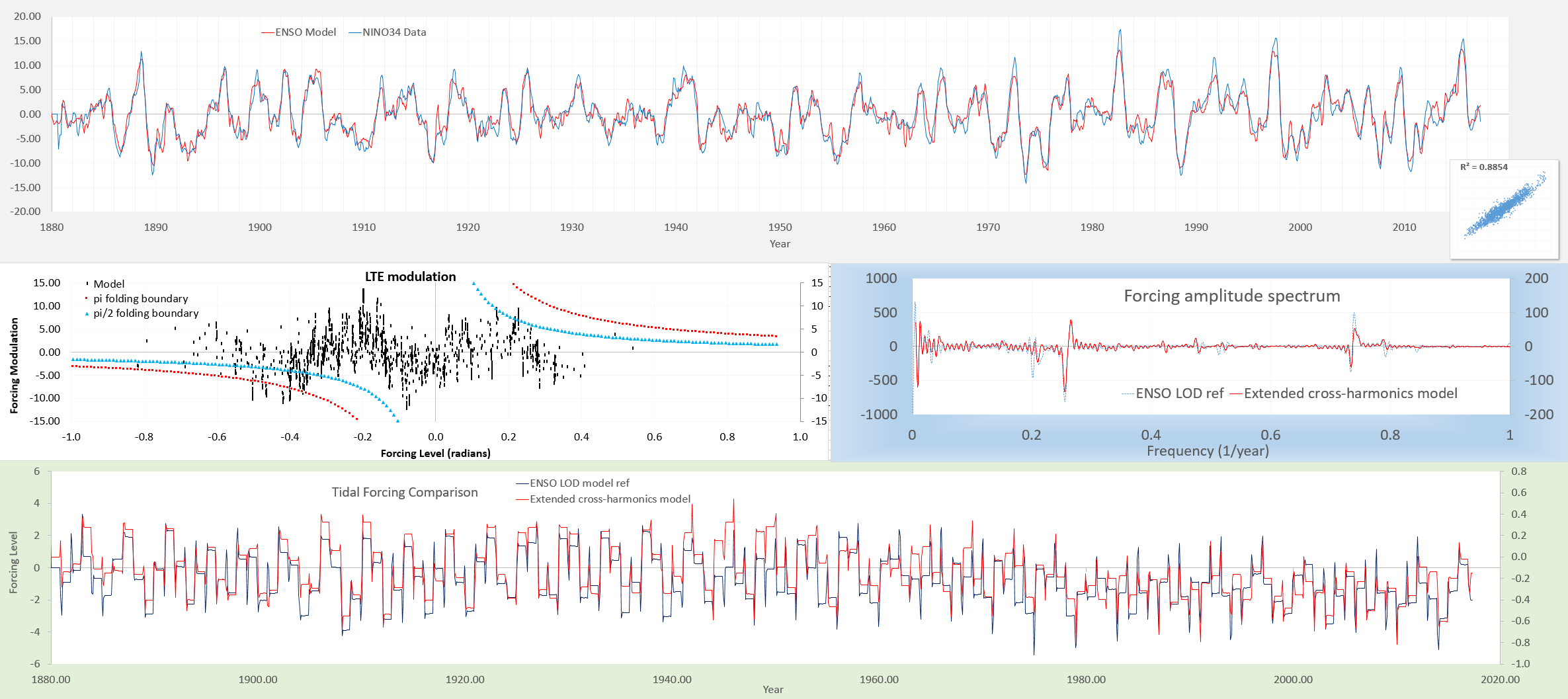
These extra harmonics also helps in matching to the much more busy SOI time-series. Click on the chart below to inspect how the higher-K wavenumbers may be the origin of what is thought to be noise in the SOI measurements.

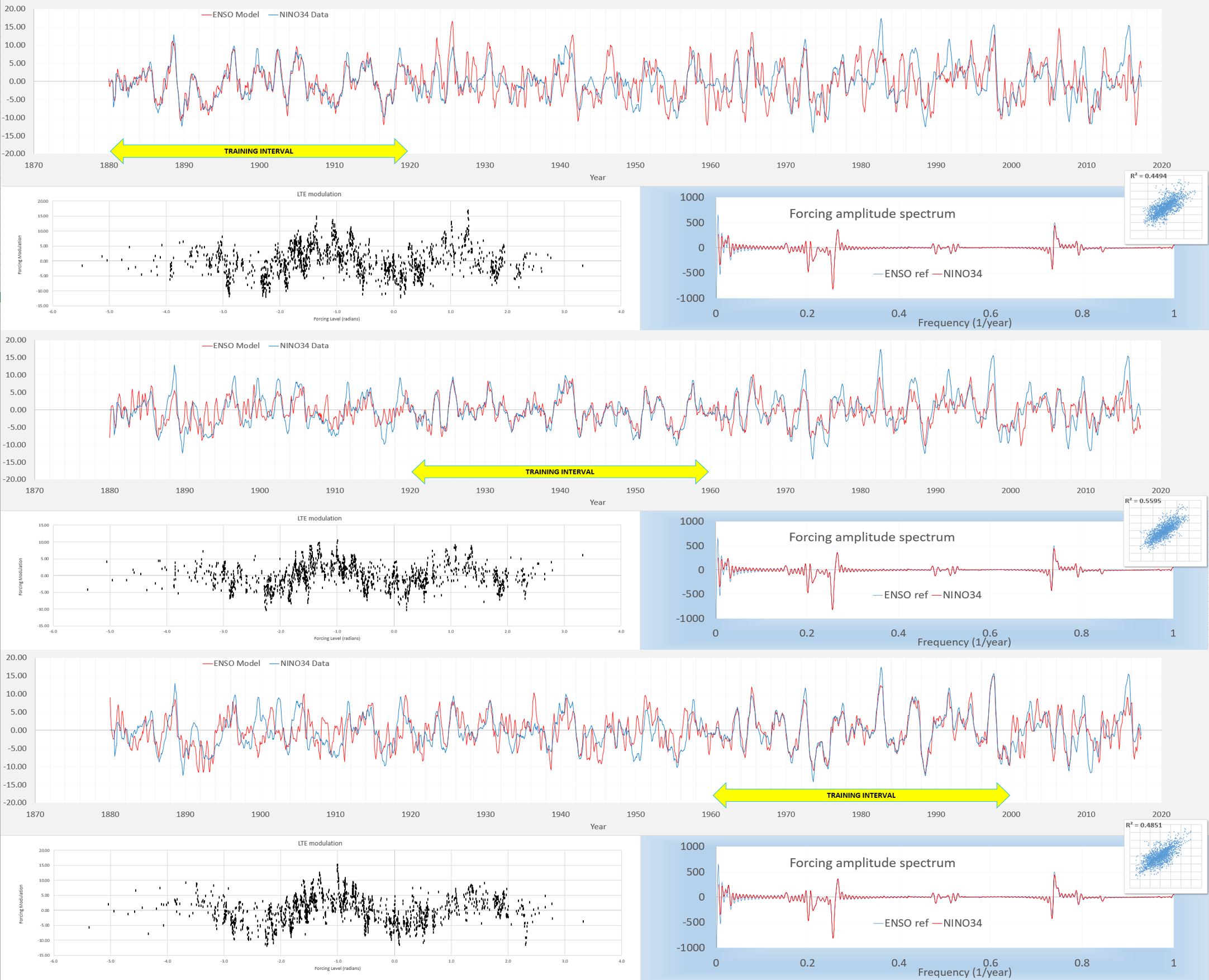
Is this a case of overfitting? Try the following cross-validation on orthogonal intervals, and note how tight the model matches the data to the training intervals, without degrading too much on the outer validation region.

I will likely add this combinatorial expansion approach to the LTE fitting software on GitHub soon, but thought to checkpoint the interim progress on the blog. In the end the likely modeling mix will be a combination of the geophysical calibration to the known dLOD response together with a refined collection of these 2nd-order combinatorial tidal constituents. The rationale for why certain terms are important will eventually become more clear as well.

References

  1. Ray, R.D. and Erofeeva, S.Y., 2014. Long‐period tidal variations in the length of day. Journal of Geophysical Research: Solid Earth, 119(2), pp.1498-1509.

Length of Day II

/ Paul Pukite (@whut) / 6 Comments

This is a continuation from the previous Length of Day post showing how closely the ENSO forcing aligns to the dLOD forcing.

Ding & Chao apply an AR-z technique as a supplement to Fourier and Max Entropy spectral techniques to isolate the tidal factors in dLOD

The red data points are the spectral values used in the ENSO model fit.

The top panel below is the LTE modulated tidal forcing fitted against the ENSO time series. The lower panel below is the tidal forcing model over a short interval overlaid on the dLOD/dt data.

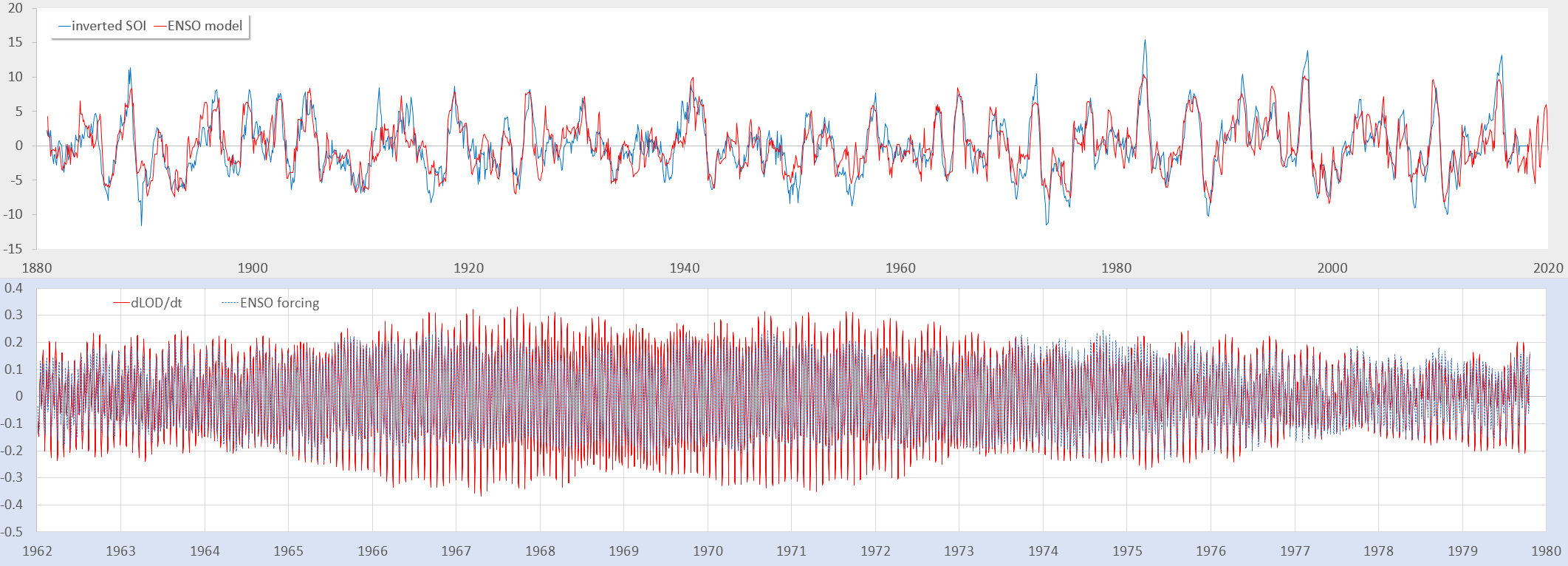
That’s all there is to it — it’s all geophysical fluid dynamics. Essentially the same tidal forcing impacts both the rotating solid earth and the equatorial ocean, but the ocean shows a lagged nonlinear response as described in Chapter 12 of the book. In contrast, the solid earth shows an apparently direct linear inertial response. Bottom line is that if one doesn’t know how to do the proper GFD, one will never be able to fit ENSO to a known forcing.

The MJO

/ Paul Pukite (@whut) / 10 Comments

In Chapter 12 of the book, we presented a math model for the equatorial Pacific ocean dipole known as ENSO (El Nino /Southern Oscillation).  We argued that the higher wavenumber (×15 of the fundamental) characteristic of ENSO was related to the behavior known as Tropical Instability Waves (TIW). Taken together, the fundamental and TIW components provide enough detail to model ENSO at the monthly level. However if we drill deeper, especially with respect to the finer granularity SOI measure of ENSO, there are rather obvious cyclic factors in the 30 to 90 day range that can add even further detail. The remarkable aspect is that these appear to be related to the behavior known as the Madden-Julian Oscillation (MJO), identified originally as a 40-50 day oscillation in zonal wind [1].

Continue reading →

Implicit Interpolating Cross-Validation of ENSO

/ Paul Pukite (@whut) / 2 Comments

In Chapter 12 of the book, we describe the forcing mechanism behind the El Nino / Southern Oscillation (ENSO) behavior and here we continue to evaluate the rich dynamic behavior of the Southern Oscillation Index (SOI) — the pressure dipole measure of ENSO. In the following, we explore how the low-fidelity version of the SOI can reveal the high-frequency content via the solution to Laplace’s Tidal Equations.

Continue reading →