For the solution to Laplace’s Tidal Equation described in Chapter 12, the spatial and temporal results are separable, leading to a non-linear standing-wave time-series formulation:

sin(kx) sin(A sin(wt) )

By analogy to a linear standing-wave formulation, a solution such as

sin(kx) sin(wt)

with the following traveling wave solution (propagating in the +x direction):

sin(kx-wt)

becomes the following in the non-linear LTE solution mode:

sin(kx – A sin(wt) )

This is also a traveling wave, but with the characteristic property of being able to periodically reverse direction from +x to –x depending on the value of A and w. As an intuitive aid, a standing wave can be considered as the superposition of two traveling waves traveling in opposite directions:

sin(kx – A sin(wt) ) + sin(kx + A sin(wt) )

Here the cross terms cancel after applying the trig identity on sums, and the separable standing-wave result similar to the first equation results. But, whenever there is an imbalance of +x and -x travelling waves, a periodic reversing traveling-wave/standing-wave mix results. This is shown in the following animation, where a mix of nonlinear traveling-waves and standing-waves show the periodic reversal in direction quite clearly.

This reversal is actually observed in ocean measurements, as exemplified in this recent research article:

• Delpech, A., Cravatte, S., Marin, F., Ménesguen, C. & Morel, Y. Deep Eddy Kinetic Energy in the Tropical Pacific From Lagrangian Floats. Journal of Geophysical Research: Oceans 125, e2020JC016313 (2020).

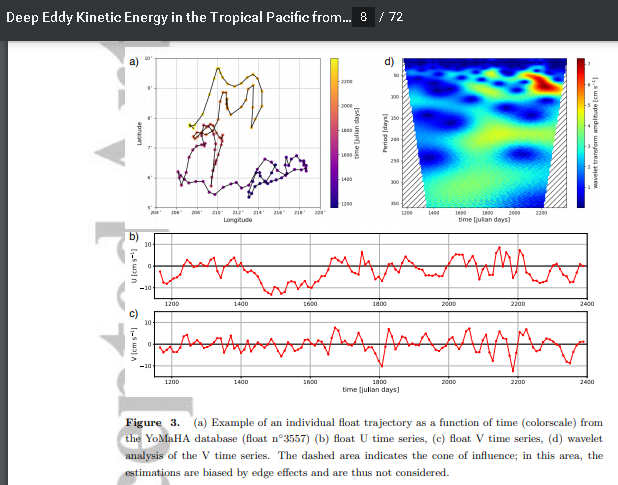
From their Figure 3, one can see this reversing process as the trajectory of a measured Argo float drift:

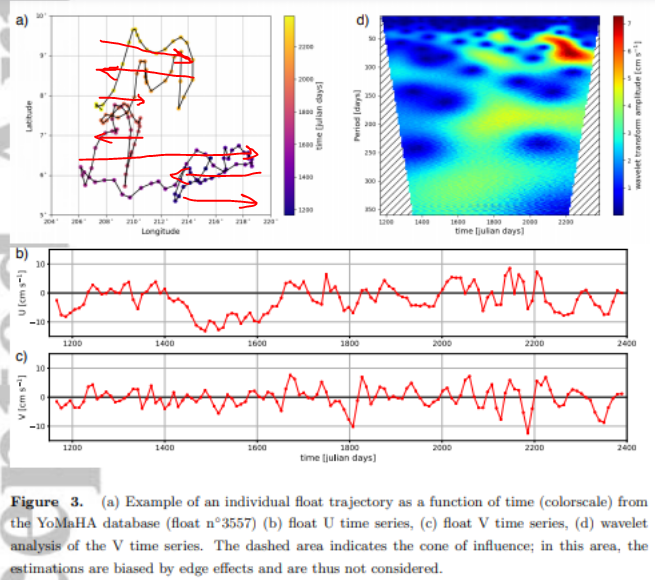
If that is not clear enough, the red arrows in the following annotated figure show the direction of the float motion. The drifting floats may not always exactly follow a trajectory as dictated by the velocity of a traveling wave, as this is partly a phase velocity with limited lateral volume displacement, but clearly a large wave-train such as a Tropical Instability Wave will certainly move a float. At least some of this is due to eddy behavior as the reversal is a natural consequence of a circular vortex motion of a large eddy.

Applying the LTE model to complete spatio-temporal data sets such as what Figure 3 is derived from would likely show an interesting match, adding value to the latest ENSO results, but this will require some digging into the data availability.