For the tidal forcing that contributes to length-of-day (LOD) variations [1], only a few factors contribute to a plurality of the variation. These are indicated below by the highlighted circles, where the V₀/g amplitude is greatest. The first is the nodal 18.6 year cycle, indicated by the N’ = 1 Doodson argument. The second is the 27.55 day “Mm” anomalistic cycle which is a combination of the perigean 8.85 year cycle (p = -1 Doodson argument) mixed with the 27.32 day tropical cycle (s=1 Doodson argument). The third and strongest is twice the tropical cycle (therefore s=2) nicknamed “Mf”.

These three factors also combine as the primary input forcing to the ENSO model. Yet, even though they are strongest, the combinatorial factors derived from multiplying these main harmonics are vital for generating a quality fit (both for dLOD and even more so for ENSO). What I have done in the past was apply the recommended mix of first- and second-order factors that appear in the dLOD spectra for the ENSO forcing.

Yet there is another approach that makes no assumption of the strongest 2nd-order factors. In this case, one simply expands the primary factors as a combinatorial expansion of cross-terms to the 4th level — this then generates a broad mix of monthly, fortnightly, 9-day, and weekly harmonic cycles. A nested algorithm to generate the 35 constituent terms is :

Counter := 1;
for J in Constituents'Range loop
 for K in Constituents'First .. J loop 
  for L in Constituents'First .. K loop 
   for M in Constituents'First .. L loop 
      Tf := Tf + Coefficients (Counter) * Fundamental(J) * 
            Fundamental(K) * Fundamental(L) * Fundamental (M); 
      Counter := Counter + 1; 
   end loop; 
  end loop; 
 end loop; 
end loop;

This algorithm requires the three fundamental terms plus one unity term to capture most of the cross-terms shown in Table 3 above (The annual cross-terms are automatic as those are generated by the model’s annual impulse). This transforms into a coefficients array that can be included in the LTE search software.

What is missing from the list are the evection terms corresponding to 31.812 (Msm) and 27.093 day cycles. They are retrograde to the prograde 27.55 day anomalistic cycle, so would need an additional 8.848 year perigee cycle bring the count from 3 fundamental terms to 4.

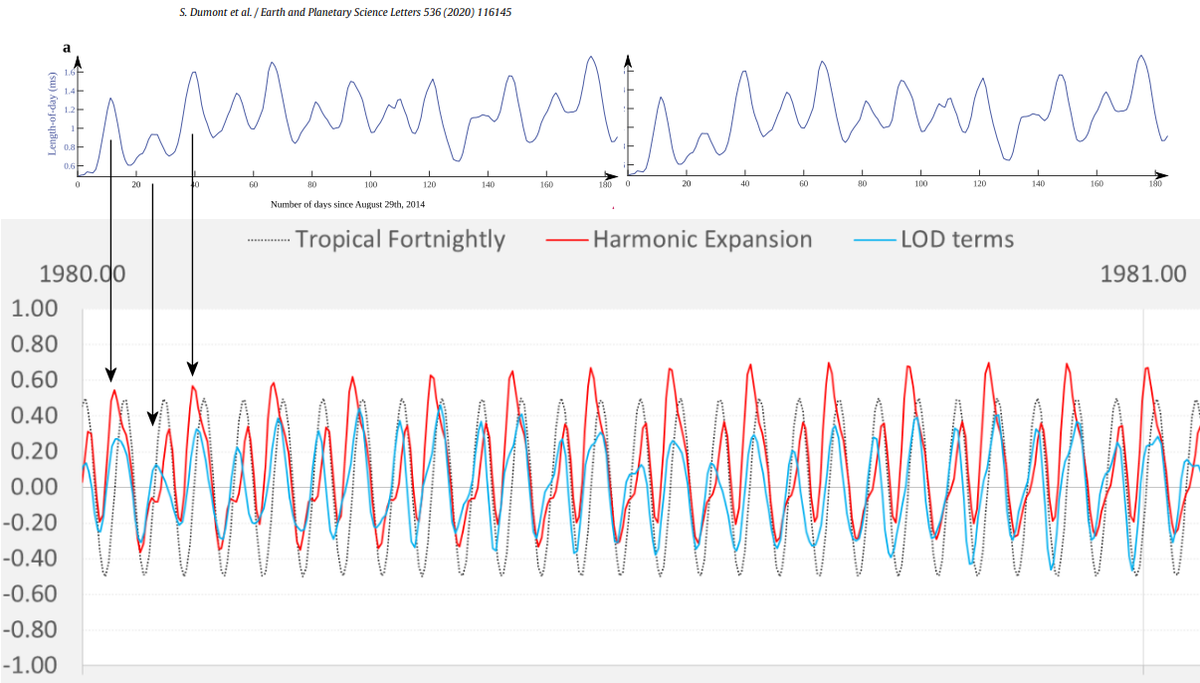
The difference between adding an extra level of harmonics, bringing the combinatorial total from 35 to 126, is not very apparent when looking at the time series (below), as it simply adds shape to the main fortnightly tropical cycle.

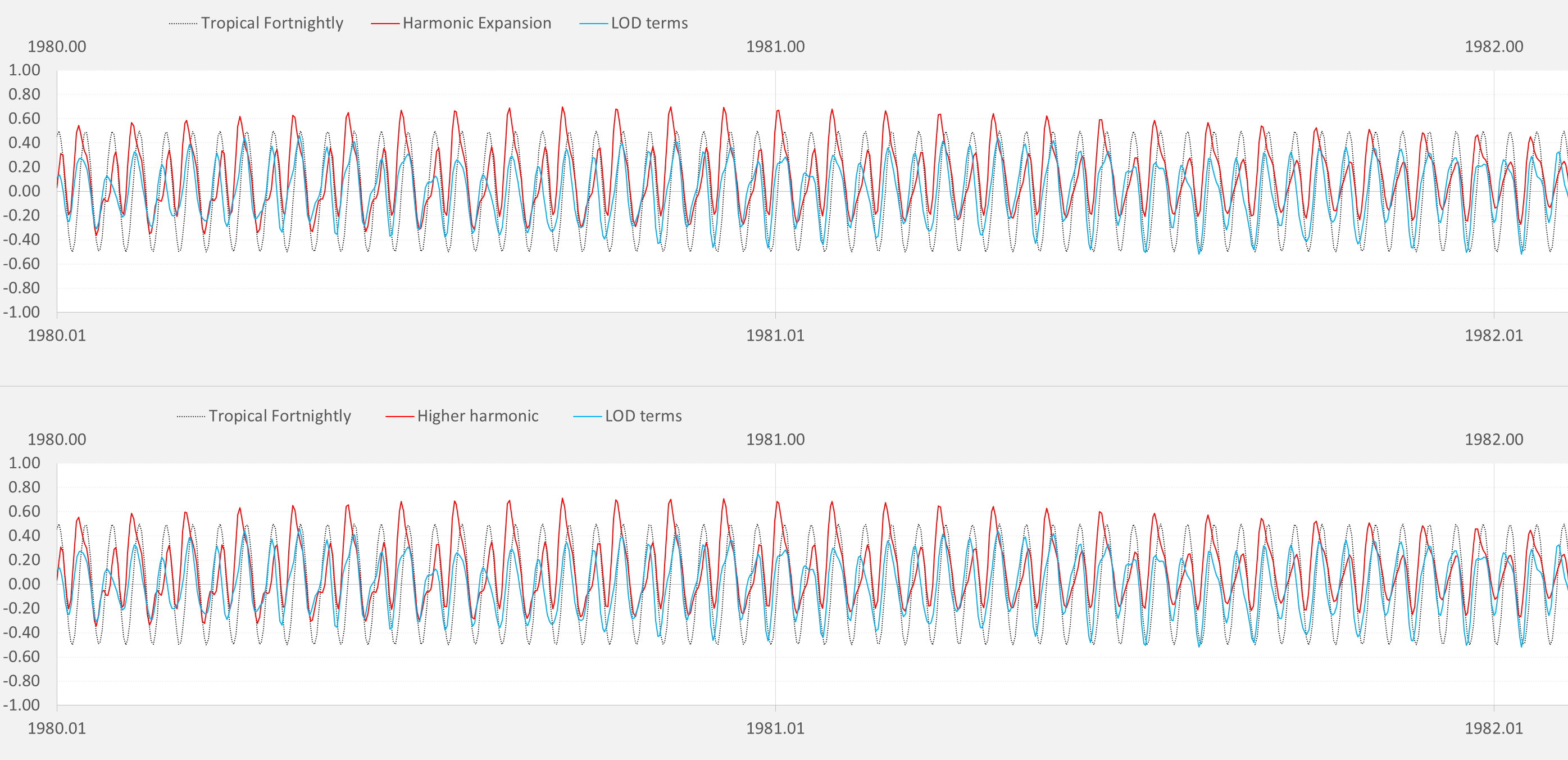
Yet it has a significant effect on the ENSO fit, approaching a CC of 0.95 (see inset at right for the scatter correlation). Note that the forcing frequency spectra in the middle right inset still shows a predominately tropical fortnightly peak at 0.26/yr and 0.74/yr.

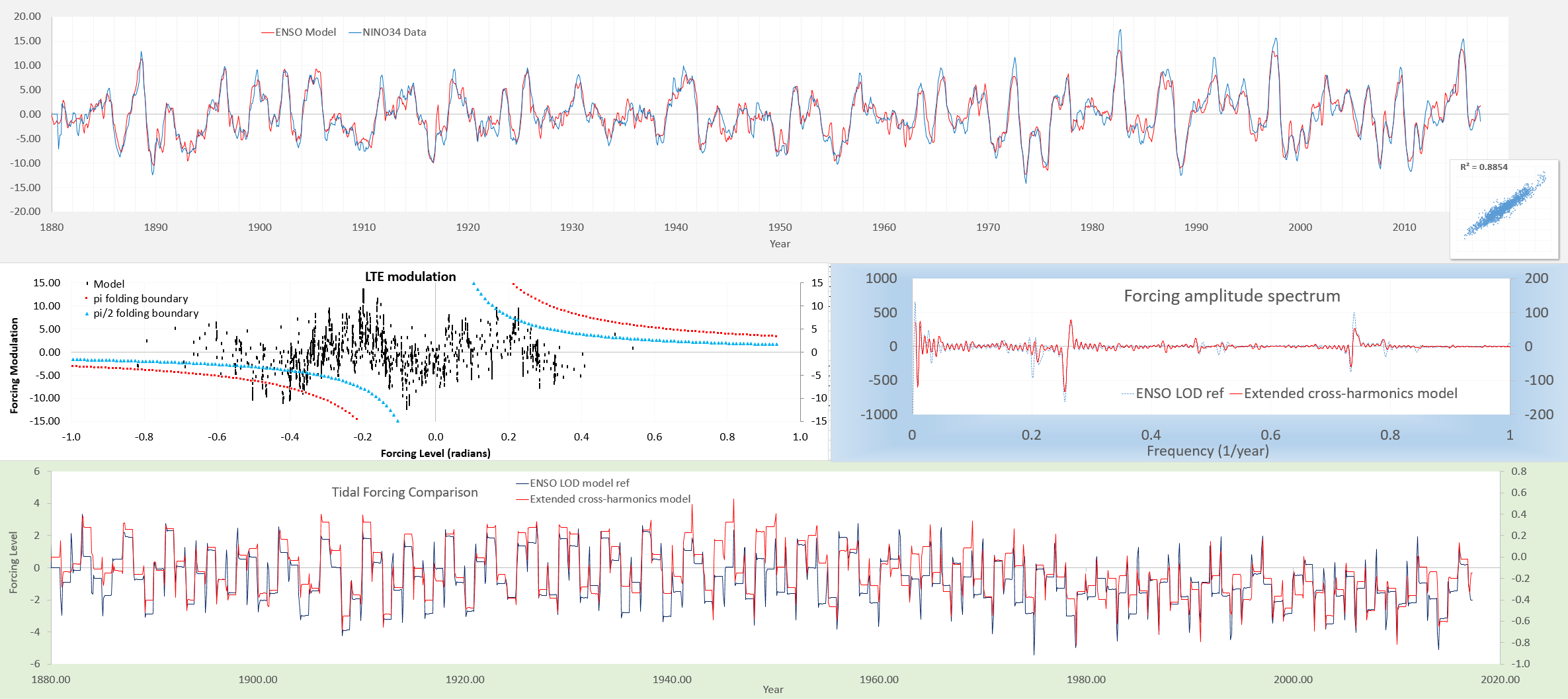
These extra harmonics also helps in matching to the much more busy SOI time-series. Click on the chart below to inspect how the higher-K wavenumbers may be the origin of what is thought to be noise in the SOI measurements.

Is this a case of overfitting? Try the following cross-validation on orthogonal intervals, and note how tight the model matches the data to the training intervals, without degrading too much on the outer validation region.

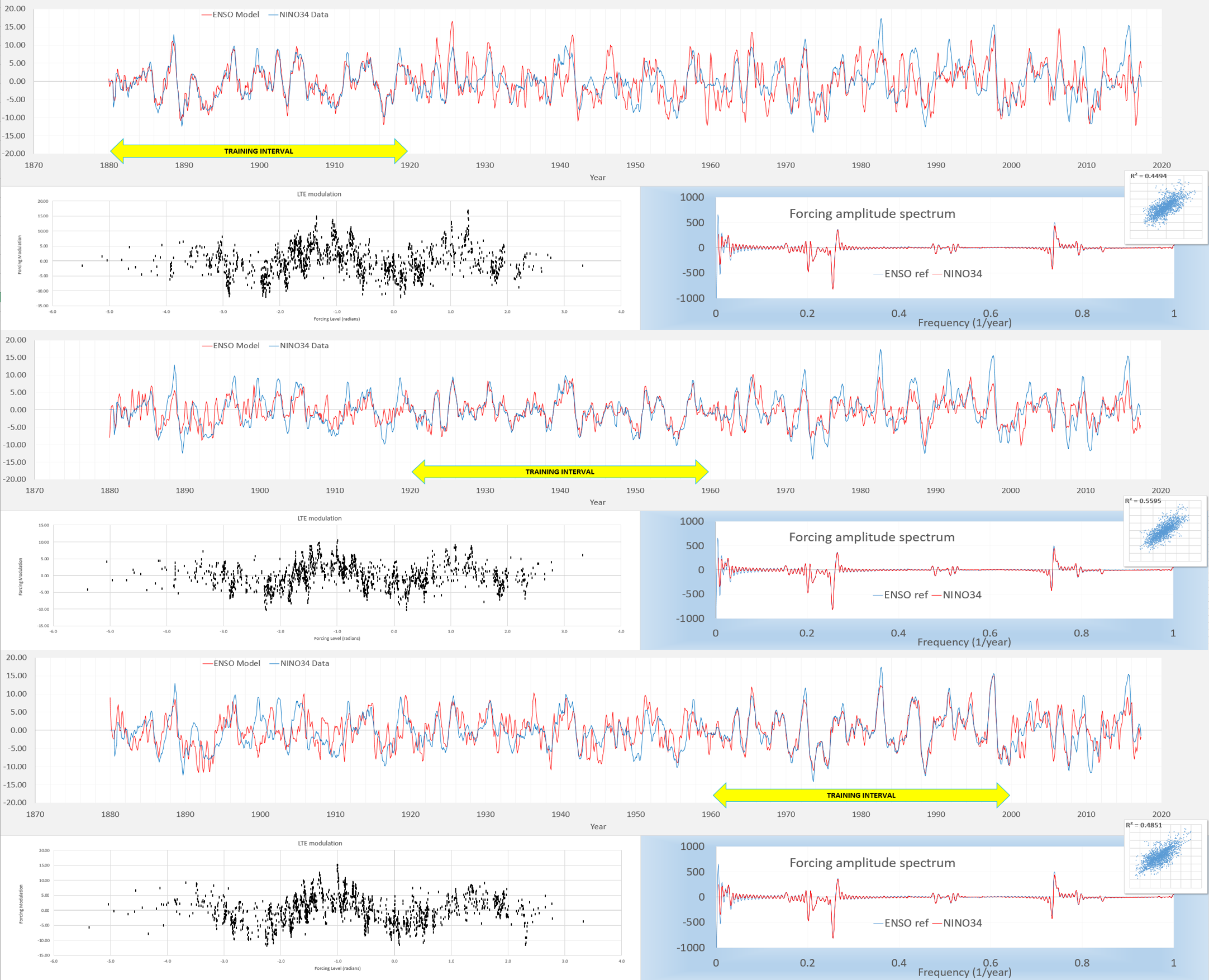
I will likely add this combinatorial expansion approach to the LTE fitting software on GitHub soon, but thought to checkpoint the interim progress on the blog. In the end the likely modeling mix will be a combination of the geophysical calibration to the known dLOD response together with a refined collection of these 2nd-order combinatorial tidal constituents. The rationale for why certain terms are important will eventually become more clear as well.

References

1. Ray, R.D. and Erofeeva, S.Y., 2014. Long‐period tidal variations in the length of day. Journal of Geophysical Research: Solid Earth, 119(2), pp.1498-1509.