I’m looking at side-band variants of the lunisolar orbital forcing because that’s where the data is empirically taking us. I had originally proposed solving Laplace’s Tidal Equations (LTE) using a novel analytical derivation published several years ago (see Mathematical Geoenergy, Wiley/AG, 2019). The takeaway from the math results — given that LTEs form the primitive basis of the GCM-specific shallow-water approximation to oceanic fluid dynamics — was that my solution involved a specific type of non-linear modulation or amplification of the input tidal. However, this isn’t the typical diurnal/semi-diurnal tidal forcing, but because of the slower inertial response of the ocean volume, the targeted tidal cycles are the longer period monthly and annual. Moreover, as very few climate scientists are proficient at signal processing and all the details of aliasing and side-bands, this is an aspect that has remained hidden (again thank Richard Lindzen for opening the book on tidal influences and then slamming it shut for decades).
Continue readinglunar
Bay of Fundy subbands

With the recent total solar eclipse, it revived lots of thought of Earth’s ecliptic plane. In terms of forcing, having the Moon temporarily in the ecliptic plane and also blocking the sun is not only a rare and (to some people) an exciting event, it’s also an extreme regime wrt to the Earth as the combined reinforcement is maximized.
In fact this is not just any tidal forcing — rather it’s in the class of tidal forcing that has been overlooked over time in preference to the conventional diurnal tides. As many of those that tracked the eclipse as it traced a path from Texas to Nova Scotia, they may have noted that the moon covers lots of ground in a day. But that’s mainly because of the earth’s rotation. To remove that rotation and isolate the mean orbital path is tricky. And that’s the time-span duration where long-period tidal effects and inertial motion can build up and show extremes in sea-level change. Consider the 4.53 year extreme tidal cycle observed at the Bay of Fundy (see Desplanque et al) located in Nova Scotia. This is predicted if the long-period lunar perigee anomaly (27.554 days and the 8.85 absidal precessional return cycle) amplifies the long period lunar ecliptic nodal cycle, as every 9.3 years the lunar path intersects the ecliptic plane, one ascending and the other descending as the moon’s gravitational pull directly aligns with the sun’s. The predicted frequencies are 1/8.85 ± 2/18.6 = 1/4.53 & 1/182, the latter identified by Keeling in 2000. The other oft-mentioned tidal extreme is at 18.6 years, which is identified as the other long period extreme at the Bay of Fundy by Desplanque, and that was also identified by NASA as an extreme nuisance tide via a press release and a spate of “Moon wobble” news articles 3 years ago.
What I find troubling is that I can’t find a scholarly citation where the 4.53 year extreme tidal cycle is explained in this way. It’s only reported as an empirical observation by Desplanque in several articles studying the Bay of Fundy tides.
Continue readingProof for allowed modes of an ideal QBO
In formal mathematical terms of geometry/topology/homotopy/homology, let’s try proving that a wavenumber=0 cycle of east/west direction inside an equatorial toroidal-shaped waveguide, can only be forced by the Z-component of a (x,y,z) vector where x,y lies in the equatorial plane.
To address this question, let’s dissect the components involved and prove within the constraints of geometry, topology, homotopy, and homology, focusing on valid mathematical principles.
Continue readingAre the QBO disruptions anomalous?
Based on the previous post on applying Dynamic Time Warping as a metric for LTE modeling of oceanic indices, it makes sense to apply the metric to the QBO model of atmospheric winds. A characteristic of QBO data is the sharp transitions of wind reversals. As described previously, DTW allows a fit to adjust the alignment between model and data without incurring a potential over-fitting penalty that a conventional correlation coefficient will often lead to.
Continue readingFull Wave Forcing
Unified Model of Earth Dynamics
Lorenz turned out to be a chaotic dead-end in understanding Earth dynamics. Instead we need a new unified model of solid liquid dynamics focusing on symmetries of the rotating earth, applying equations of solid bodies & fluid dynamics. See Mathematical Geoenergy (Wiley, 2018).
Should have made this diagram long ago: here’s the ChatGPT4 prompt with the diagramming plugin.
Graph

Ocean Tides and dLOD have always been well-understood, largely because the mapping to lunar+solar cycles is so obvious. And the latter is getting better all the time — consider recent hi-res LOD measurements with a ring laser interferometer, pulling in diurnal tidal cycles with much better temporal resolution.

That’s the first stage of unification (yellow boxes above) — next do the other boxes (CW, QBO, ENSO, AMO, PDO, etc) as described in the book and on this blog, while calibrating to tides and LOD, and that becomes a cross-validated unified model.
Annotated 10/11/2023
ontological classification according to wavenumber kx, ky, kz and fluid/solid.

Added so would not lose it — highlighted tidal factor is non-standard

Paleo ENSO
Two recent articles prompted a few ideas
From last year, https://watchers.news/2022/11/10/study-shows-how-earth-sun-distance-dramatically-influences-annual-weather-cycles-in-the-equatorial-pacific-in-a-22-000-year-cycle/ points to:
Two annual cycles of the Pacific cold tongue under orbital precession
Which says that
“Because the distance effect annual cycle (from perihelion to perihelion, otherwise called the anomalistic year, 365.259636 d (ref. 6)) is slightly longer than the tilt effect annual cycle (from equinox to equinox, otherwise known as the tropical year, 365.242189 d (ref. 6)), the LOP increases over time. A complete revolution of the LOP is the precession cycle, about 22,000 yr (ref. 38). “
The claim is that the exact timing and strength of the annual cycle extreme is important in initiating an El Nino or La Nina cycle. as the Longitude of Perihelion (LOP) moves over time, so that when this aligns with the solstice/equinox events, the ENSO behavior will mirror the strength of the forcing.

Next article
ENSO-related centennial and millennialscale hydroclimate changes recorded from Lake Xiaolongchi in arid Central Asia over the past 8000 years
They note 800 year cycles in the observations

This is not a 22,000 year cycle (as stated its actuallly closer to 21,000), but it’s possible that if tidal cycles play a part of the forcing, then a much shorter paleo cycle may emerge. Consider that the Mf tidal cycle of 13.66 days will generate a cycle of ~3.81 years when non-linearly modulated against the tropical year (seasonal cycle), but ~3.795 years modulated against the perigean or anomalistic year (nearest approach to the sun).

The difference between the two will reinforce every 783 years, which is close to the 800 year cycle. Aliasing and sideband frequency calculations reveal these patterns.
Wobble Perturbation
After this point, I provided ChatGPT prompts as italicized underlines after each sinewave icon ![]()
![]() , and ChatGPT provided responses. I executed the Julia code in a REPL window and saved the screenshotted plots and entered the image links below.
, and ChatGPT provided responses. I executed the Julia code in a REPL window and saved the screenshotted plots and entered the image links below.
Model: GPT-4
Math equations for a spinning top in Julia
To simulate a spinning top in Julia, you can use the equations of motion derived from Euler’s equations for a rigid body. Here’s a simple example using the DifferentialEquations.jl package, which provides a convenient way to solve ordinary differential equations (ODEs) in Julia:
- First, install the required packages by running:
using Pkg
Pkg.add("DifferentialEquations")
Pkg.add("Plots")
- Now, you can write a script to simulate a spinning top:
using DifferentialEquations
using Plots
# Define the spinning top's properties
I1, I2, I3 = 0.1, 0.2, 0.3 # Moments of inertia along the principal axes (x, y, z)
Ω1, Ω2, Ω3 = 0.0, 10.0, 20.0 # Initial angular velocities (rad/s)
# Equations of motion for the spinning top (Euler's equations for a rigid body)
function spinning_top!(du, u, p, t)
Ω1, Ω2, Ω3 = u
du[1] = (I2 - I3)/I1 * Ω2 * Ω3
du[2] = (I3 - I1)/I2 * Ω1 * Ω3
du[3] = (I1 - I2)/I3 * Ω1 * Ω2
end
# Initial conditions
u0 = [Ω1, Ω2, Ω3]
tspan = (0.0, 10.0) # Time span for the simulation (in seconds)
# Solve the ODE
prob = ODEProblem(spinning_top!, u0, tspan)
sol = solve(prob, Tsit5(), reltol=1e-8, abstol=1e-8)
# Plot the angular velocities
plot(sol, xlabel="Time (s)", ylabel="Angular velocity (rad/s)", title="Spinning Top", legend=:bottomright)
This code sets up and solves the ODEs that describe the motion of a spinning top with specified moments of inertia and initial angular velocities. The result is then plotted to show the evolution of the angular velocities over time.
Remember that this is a simple example that assumes the top is spinning in a vacuum, without any external forces or torques acting on it (such as gravity or air resistance). To model a more realistic spinning top, you will need to account for these factors in your equations of motion.
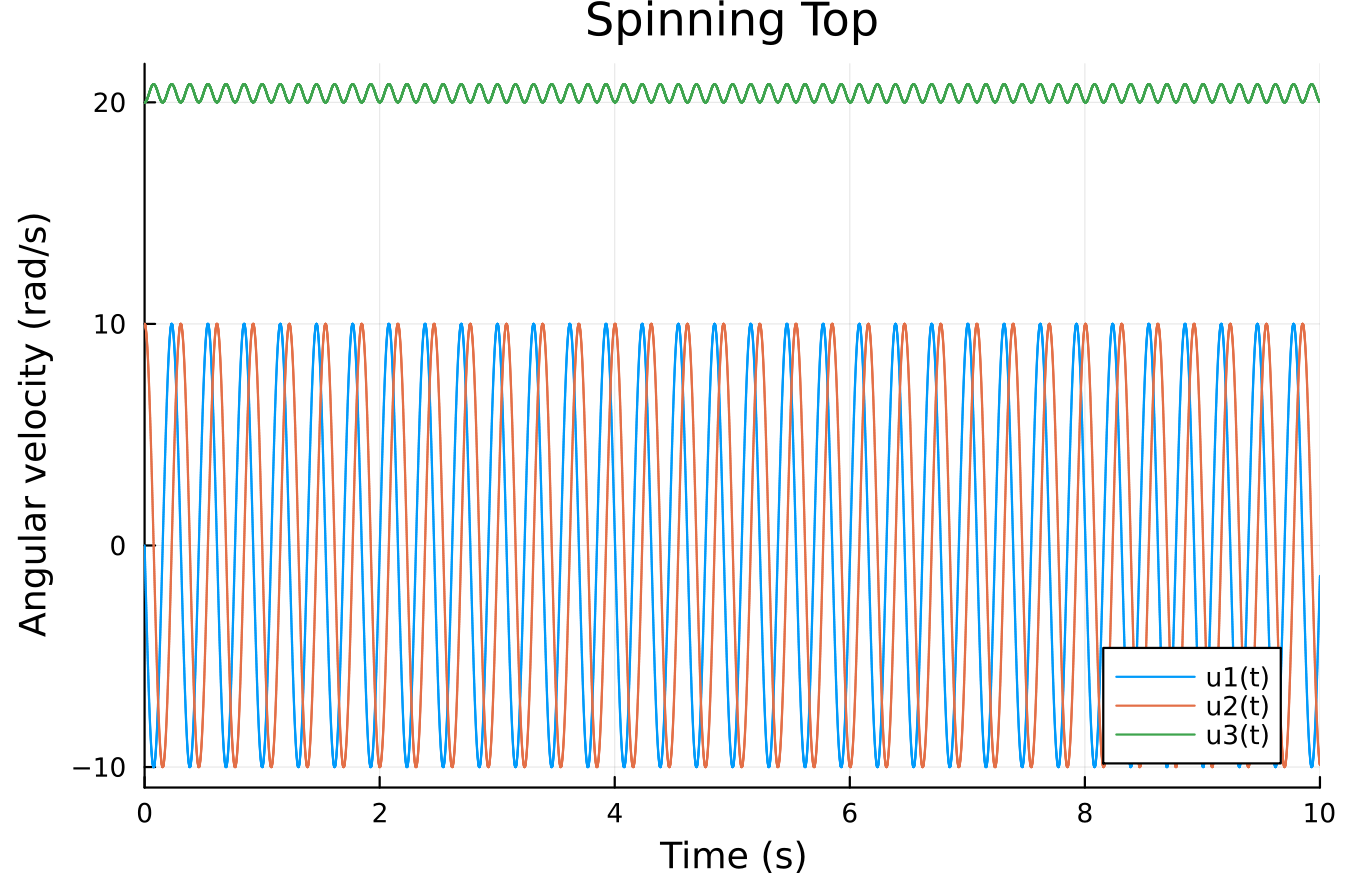
To the equations, add a slight periodic horizontal forcing impulse to the top of the spinning top
To add a slight periodic horizontal forcing impulse to the spinning top, you can modify the equations of motion accordingly. Let’s assume the forcing impulse acts along the x-axis and has the form F(t) = F0 * sin(ω * t), where F0 is the amplitude of the forcing impulse and ω is its angular frequency.
Here’s how you can update the spinning top simulation:
- Modify the spinning_top! function to include the forcing impulse:
function spinning_top!(du, u, p, t)
Ω1, Ω2, Ω3 = u
F0, ω, I1, I2, I3 = p
# Forcing impulse along the x-axis
F = F0 * sin(ω * t)
du[1] = (I2 - I3)/I1 * Ω2 * Ω3 + F/I1
du[2] = (I3 - I1)/I2 * Ω1 * Ω3
du[3] = (I1 - I2)/I3 * Ω1 * Ω2
end
- Update the initial conditions and ODE problem:
# Forcing impulse parameters
F0 = 0.01 # Amplitude of the forcing impulse
ω = 2π / 5 # Angular frequency of the forcing impulse (period = 5 seconds)
# Parameters to be passed to the spinning_top! function
p = [F0, ω, I1, I2, I3]
# Solve the ODE
prob = ODEProblem(spinning_top!, u0, tspan, p)
sol = solve(prob, Tsit5(), reltol=1e-8, abstol=1e-8)
The updated spinning_top! function now includes a forcing impulse along the x-axis, which is passed as a parameter (F0, ω). The ODE problem is also updated to include these parameters.
By running the simulation with the updated code, you can observe the effects of the slight periodic horizontal forcing impulse on the spinning top.
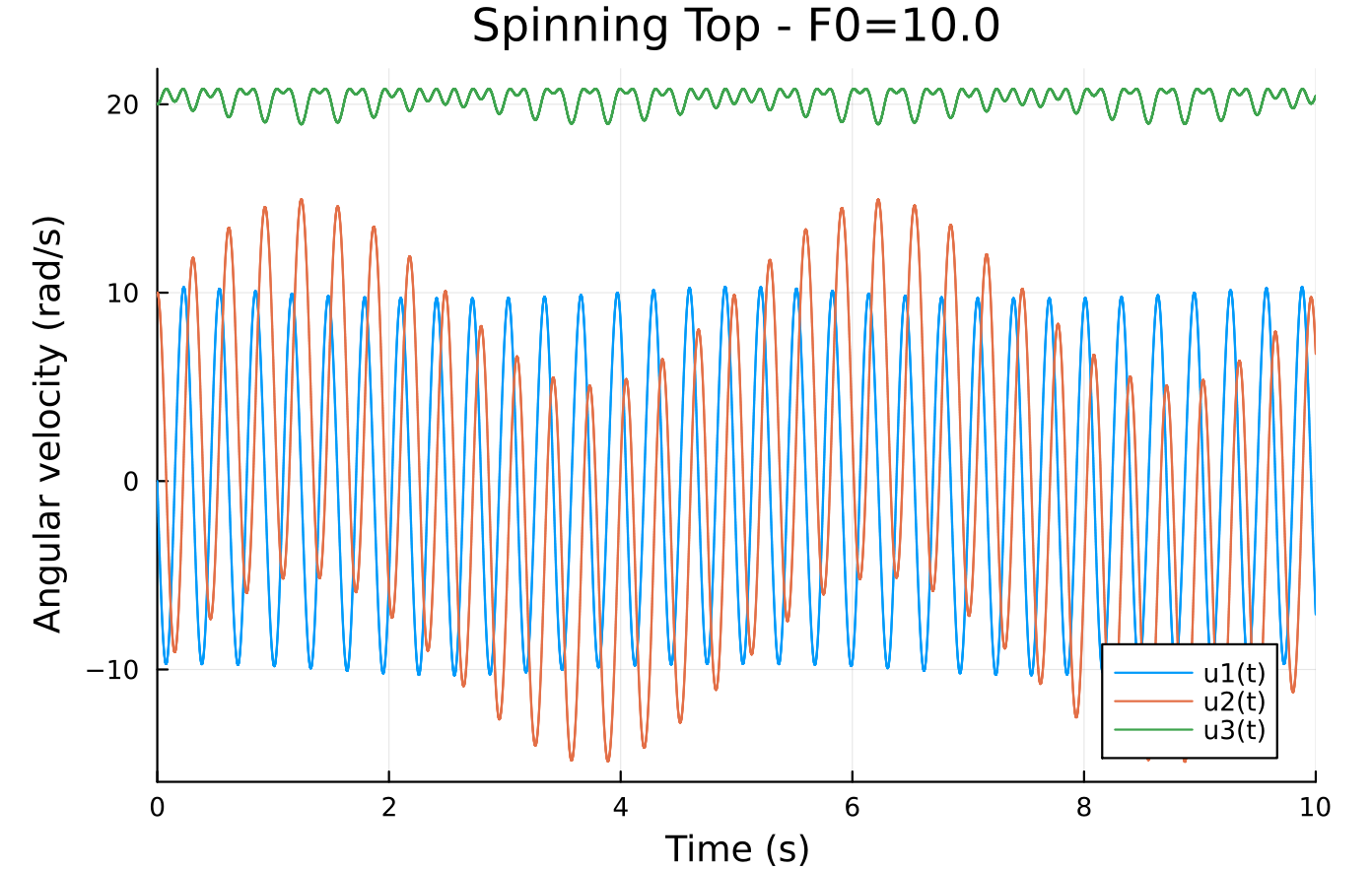
Is there an analytical solution for small forcing perturrbations?
For small forcing perturbations, it may be possible to find an approximate analytical solution using perturbation methods, such as regular perturbation or multiple-scale perturbation techniques. These methods involve expanding the solution in a power series of a small parameter (in this case, the amplitude of the forcing perturbation) and then substituting the series into the equations of motion.
However, finding an exact analytical solution for the spinning top with small forcing perturbations is generally not feasible due to the nonlinear nature of the governing equations. The Euler equations for rigid body rotation are a set of coupled, nonlinear ordinary differential equations, and the addition of a forcing term makes them even more complex. In practice, numerical methods are often used to solve these equations, as demonstrated in the previous examples.
If you want to gain insights into the behavior of the system under small forcing perturbations, you can use linear stability analysis and perturbation methods to study the stability and dynamics of the system. These methods can help you find approximate analytical solutions that are valid for small perturbations and understand the qualitative behavior of the system. However, for a complete and accurate description of the spinning top’s motion with forcing, it is usually necessary to rely on numerical simulations.
Generate the equivalent Fourier series representation of the previous differential equations.
A Fourier series representation is typically used to approximate periodic functions. In this case, we have a system of differential equations describing the motion of a spinning top with a forcing term. Instead of directly finding a Fourier series representation for the differential equations, we can approximate the solution of the system using a Fourier series.
To do this, we can first find the solution of the system without the forcing term (i.e., the homogeneous solution) and then find the particular solution that results from the forcing term. Finally, we can approximate both the homogeneous and particular solutions using Fourier series and combine them to obtain an approximation of the total solution.
Here’s a general outline of the approach:
- Solve the homogeneous system (i.e., without the forcing term) to find the homogeneous solution.
- Assume a particular solution of the form:
Ω1(t) = A1 * sin(ω * t) + B1 * cos(ω * t)
Ω2(t) = A2 * sin(ω * t) + B2 * cos(ω * t)
Ω3(t) = A3 * sin(ω * t) + B3 * cos(ω * t)
where A1, B1, A2, B2, A3, and B3 are constants to be determined. - Substitute the particular solution into the differential equations with the forcing term and solve for the constants A1, B1, A2, B2, A3, and B3.
- Approximate the homogeneous and particular solutions using Fourier series, and combine them to obtain an approximation of the total solution.
Please note that this approach involves several steps and requires solving multiple linear systems and integrals to find the Fourier coefficients. Due to the complexity of the Euler equations and the forcing term, it may be challenging to find an exact analytical solution, even using the Fourier series approximation. In practice, numerical methods are often used to solve such systems, as demonstrated in the previous examples.
Assume the homogeneous solution damps out and only the particular solution remains, so find the steady-state solution only.
To find the steady-state solution, we’ll focus on the particular solution with the forcing term, as the homogeneous solution is assumed to damp out. We’ll assume a particular solution of the form:
Ω1(t) = A1 * sin(ω * t) + B1 * cos(ω * t)
Ω2(t) = A2 * sin(ω * t) + B2 * cos(ω * t)
Ω3(t) = A3 * sin(ω * t) + B3 * cos(ω * t)
Differentiating Ω1(t), Ω2(t), and Ω3(t) with respect to time, we get:
dΩ1/dt = ω * (A1 * cos(ω * t) – B1 * sin(ω * t))
dΩ2/dt = ω * (A2 * cos(ω * t) – B2 * sin(ω * t))
dΩ3/dt = ω * (A3 * cos(ω * t) – B3 * sin(ω * t))
Substitute these expressions into the modified Euler equations with the forcing term:
(1) (I2 – I3)/I1 * Ω2 * Ω3 + F/I1 = dΩ1/dt
(2) (I3 – I1)/I2 * Ω1 * Ω3 = dΩ2/dt
(3) (I1 – I2)/I3 * Ω1 * Ω2 = dΩ3/dt
Now, we can solve for the unknown coefficients A1, B1, A2, B2, A3, and B3 by substituting the particular solution and its derivatives into these equations and equating the coefficients of the sine and cosine terms. This will result in a system of linear equations that can be solved analytically or numerically.
However, due to the complexity of these equations and the nonlinear interaction between Ω1, Ω2, and Ω3, finding an exact analytical solution for the coefficients may be difficult. In practice, it is often more convenient to use numerical methods, such as the ones shown in the previous examples, to find the steady-state solution of the spinning top system under periodic forcing.
Calculate if one of the moments of inertia is much larger than the other two.
If one of the moments of inertia is much larger than the other two, the behavior of the spinning top can be significantly different. Let’s assume I3 is much larger than I1 and I2, i.e., I3 >> I1, I2. The modified Euler equations with the forcing term are:
(1) (I2 – I3)/I1 * Ω2 * Ω3 + F/I1 = dΩ1/dt
(2) (I3 – I1)/I2 * Ω1 * Ω3 = dΩ2/dt
(3) (I1 – I2)/I3 * Ω1 * Ω2 = dΩ3/dt
Since I3 is much larger than I1 and I2, we can make the following approximations:
- The term (I2 – I3)/I1 ≈ -1 and (I3 – I1)/I2 ≈ 1, as I3 dominates both I1 and I2.
- The term (I1 – I2)/I3 becomes very small and can be neglected.
Now, the modified Euler equations can be simplified as:
(1) -Ω2 * Ω3 + F/I1 = dΩ1/dt
(2) Ω1 * Ω3 = dΩ2/dt
(3) 0 ≈ dΩ3/dt
Since dΩ3/dt is approximately zero, we can assume that Ω3 remains constant in the steady-state, i.e., the angular velocity about the z-axis remains constant.
Now, we can focus on finding the steady-state solution for Ω1(t) and Ω2(t) only. Assuming a particular solution of the form:
Ω1(t) = A1 * sin(ω * t) + B1 * cos(ω * t)
Ω2(t) = A2 * sin(ω * t) + B2 * cos(ω * t)
Substitute these expressions and their time derivatives into equations (1) and (2). Then, equate the coefficients of sine and cosine terms to obtain a system of linear equations for the unknown coefficients A1, B1, A2, and B2.
Due to the complexity of these equations, finding an exact analytical solution for the coefficients may still be challenging. As mentioned before, using numerical methods may be more convenient to find the steady-state solution of the spinning top system under these conditions.
Will the particular solutions be composed of harmonics of ω?
Yes, the particular solutions will be composed of harmonics of ω, the frequency of the forcing term. This is because the response of the system to the forcing term will have the same frequency as the forcing term itself.
When solving for the particular solution, we assumed a form like:
Ω1(t) = A1 * sin(ω * t) + B1 * cos(ω * t)
Ω2(t) = A2 * sin(ω * t) + B2 * cos(ω * t)
Ω3(t) = A3 * sin(ω * t) + B3 * cos(ω * t)
Here, the forcing term has a frequency of ω, and the particular solution also has the same frequency. The coefficients A1, B1, A2, B2, A3, and B3 depend on the system’s parameters and the forcing term. When the system reaches a steady-state, it will exhibit a response at the same frequency as the forcing term, i.e., ω.
It is essential to note that, in some cases, the response of the system may also contain higher harmonics of the forcing frequency if the equations are nonlinear. In the case of the spinning top, the Euler equations are nonlinear, and the interaction between the angular velocities can cause higher harmonics to appear in the response. However, for small forcing amplitudes, the response is expected to be dominated primarily by the forcing frequency ω.
Calculate if the moments of inertia are ordered as follows: I3 >> I2 >> I1.
If the moments of inertia are ordered as I3 >> I2 >> I1, the behavior of the spinning top can be analyzed using the modified Euler equations with the forcing term:
(1) (I2 – I3)/I1 * Ω2 * Ω3 + F/I1 = dΩ1/dt
(2) (I3 – I1)/I2 * Ω1 * Ω3 = dΩ2/dt
(3) (I1 – I2)/I3 * Ω1 * Ω2 = dΩ3/dt
Since I3 is much larger than I1 and I2, we can approximate:
- The term (I2 – I3)/I1 ≈ -1, as I3 dominates both I1 and I2.
- The term (I3 – I1)/I2 ≈ 1, as I3 dominates I1.
Since I2 is much larger than I1, we can also approximate:
- The term (I1 – I2)/I3 ≈ -1, as I2 dominates I1.
Now, the modified Euler equations can be simplified as:
(1) -Ω2 * Ω3 + F/I1 = dΩ1/dt
(2) Ω1 * Ω3 = dΩ2/dt
(3) -Ω1 * Ω2 = dΩ3/dt
As before, we can focus on finding the steady-state solution for Ω1(t) and Ω2(t). We assume a particular solution of the form:
Ω1(t) = A1 * sin(ω * t) + B1 * cos(ω * t)
Ω2(t) = A2 * sin(ω * t) + B2 * cos(ω * t)
For Ω3(t), since dΩ3/dt is a product of Ω1 and Ω2, and both Ω1 and Ω2 have harmonic components at the frequency ω, the steady-state solution for Ω3(t) will also be composed of harmonics at the frequency ω:
Ω3(t) = A3 * sin(ω * t) + B3 * cos(ω * t)
Substitute these expressions and their time derivatives into equations (1), (2), and (3). Then, equate the coefficients of sine and cosine terms to obtain a system of linear equations for the unknown coefficients A1, B1, A2, B2, A3, and B3.
Due to the complexity of these equations, finding an exact analytical solution for the coefficients may still be challenging. As mentioned before, using numerical methods may be more convenient to find the steady-state solution of the spinning top system under these conditions.
How can the individual Euler equations reduce to identities since the RHS contains the fundamental frequency ω, while the LHS contains harmonics including 2ω due to the nonlinear product?
You’re correct in pointing out that the interaction between the angular velocities can cause higher harmonics to appear in the response due to the nonlinear nature of the Euler equations. My previous explanations did not fully capture this complexity.
Instead of directly assuming a particular solution with only the fundamental frequency ω, we should allow for the possibility of having higher harmonics in the response. To account for higher harmonics in the particular solution, we can use the following form:
Ω1(t) = ∑(A1n * cos(n * ω * t) + B1n * sin(n * ω * t))
Ω2(t) = ∑(A2n * cos(n * ω * t) + B2n * sin(n * ω * t))
Ω3(t) = ∑(A3n * cos(n * ω * t) + B3n * sin(n * ω * t))
The sum runs over all integer values of n, including the fundamental frequency and higher harmonics.
Substitute these expressions and their time derivatives into the Euler equations and then equate the coefficients of the sine and cosine terms for each harmonic. This will result in an infinite system of linear equations for the unknown coefficients A1n, B1n, A2n, B2n, A3n, and B3n.
In practice, it is not possible to solve for all these coefficients analytically, and we typically truncate the sum after a finite number of terms, capturing the most significant harmonics in the response. This will result in an approximate solution that accounts for higher harmonics due to the nonlinear product terms in the Euler equations.
The steady-state solution can then be obtained by solving the resulting truncated system of linear equations, either analytically or numerically. Note that finding the steady-state solution in this manner can still be quite challenging due to the complexity of the equations and the presence of higher harmonics. Therefore, numerical methods are often more convenient for solving such systems.
How to solve if the primary inertial moment I1 changes by a small frequency characterized by ν?
If the primary inertial moment I1 changes with a small frequency characterized by ν, we can represent I1 as a function of time:
I1(t) = I1_0 + ε * cos(ν * t)
where I1_0 is the constant mean value of I1, ε represents the amplitude of the variation, and ν is the frequency of the change.
The modified Euler equations with the forcing term now become:
(1) (I2 – I3)/I1(t) * Ω2 * Ω3 + F/I1(t) = dΩ1/dt
(2) (I3 – I1(t))/I2 * Ω1 * Ω3 = dΩ2/dt
(3) (I1(t) – I2)/I3 * Ω1 * Ω2 = dΩ3/dt
These equations are now more complex due to the time-varying nature of I1(t). To find the steady-state solution, we can assume that the response of the system will contain harmonics related to both the forcing frequency ω and the frequency ν of the changing inertia:
Ω1(t) = ∑(A1n * cos((n * ω + m * ν) * t) + B1n * sin((n * ω + m * ν) * t))
Ω2(t) = ∑(A2n * cos((n * ω + m * ν) * t) + B2n * sin((n * ω + m * ν) * t))
Ω3(t) = ∑(A3n * cos((n * ω + m * ν) * t) + B3n * sin((n * ω + m * ν) * t))
The sum runs over all integer values of n and m, including the fundamental frequency and higher harmonics.
Substitute these expressions and their time derivatives into the Euler equations, and then equate the coefficients of the sine and cosine terms for each harmonic. This will result in an infinite system of linear equations for the unknown coefficients A1n, B1n, A2n, B2n, A3n, and B3n.
In practice, we truncate the sum after a finite number of terms to capture the most significant harmonics in the response. This will result in an approximate solution that accounts for higher harmonics due to the nonlinear product terms in the Euler equations and the time-varying nature of I1.
Finding the steady-state solution in this manner can be quite challenging due to the complexity of the equations and the presence of higher harmonics. Numerical methods are often more convenient for solving such systems, and you may consider using tools like the Julia programming language or other computational methods to find an approximate solution.
.
Because of a high-Q and narrrow bandwidth of the response, will certain of these frequency terms predominate in the solution?
Yes, due to the high-Q (high quality factor) and narrow bandwidth of the response, certain frequency terms will predominate in the solution. A high-Q system is characterized by a sharp resonance peak, which means it is sensitive to a small range of frequencies around the natural frequency. As a result, only those harmonics that lie within the narrow bandwidth of the response will have a significant impact on the system’s behavior.
In the case of the spinning top with time-varying inertia, the response will be dominated by harmonics related to the forcing frequency ω and the frequency ν of the changing inertia. However, not all harmonics will have a substantial effect on the system. Those harmonics that are close to the natural frequencies of the system or within the narrow bandwidth of the response will predominate.
When solving the system of equations for the steady-state solution, you can focus on the most significant harmonics that lie within the narrow bandwidth of the response. This approach will not only reduce the complexity of the problem but also provide a more accurate approximation of the actual system behavior. You may need to analyze the system’s resonance behavior, such as by using a frequency response or a transfer function, to determine which harmonics are most important for the given problem.
Keep in mind that, even with a reduced number of terms, solving the resulting system of equations can still be quite challenging due to the nonlinear nature of the problem. Numerical methods are often more convenient for finding approximate solutions in such cases.
By replacing the spinning-top with the Earth with a slight annual time-varying inertia I1, and the small cyclical perturbing force as the Moon with a 27.2122 cycle, can we estimate the primary wobble in the Earth’s rotational axis?
To estimate the primary wobble in the Earth’s rotational axis due to the time-varying inertia I1 and the perturbing force from the Moon, we can use a simplified model based on the Earth-Moon system. We can consider the Earth as an oblate spheroid and the Moon’s gravitational influence as the perturbing force.
In this context, the Earth’s time-varying inertia I1 can be associated with the annual variations in the Earth’s shape due to seasonal changes in the distribution of mass (e.g., changes in ice and snow cover, ocean mass distribution). The Moon’s gravitational pull has a primary cycle of 27.2122 days (the sidereal month), which is the time it takes for the Moon to complete one orbit around Earth relative to the fixed stars.
The wobble in the Earth’s rotational axis, called nutation, is a small oscillation superimposed on the larger precession of the Earth’s axis. The primary wobble is caused by the combined effects of the time-varying inertia and the perturbing force from the Moon.
To estimate the primary wobble, you can use the Euler equations with the time-varying inertia and the perturbing force, similar to the spinning-top model discussed earlier. However, this approach is highly complex and requires a deep understanding of the Earth-Moon system’s dynamics and geophysics.
A more practical approach to estimate the primary wobble is to use existing models and data derived from observations of the Earth’s rotation. One such model is the International Earth Rotation and Reference Systems Service (IERS) Conventions, which provide nutation models that account for the gravitational effects of the Moon, Sun, and other celestial bodies, as well as the Earth’s time-varying inertia due to seasonal changes.
By using the IERS Conventions or similar models, you can estimate the primary wobble in the Earth’s rotational axis without solving the complex Euler equations for the Earth-Moon system. Note that such models are based on empirical data and theoretical understanding of the Earth’s rotation, so they provide an approximation of the actual wobble.
Can we calculate the primary aliased harmonic based on the combination of the Moon’s cycle and the annual cycle of I1, applying estimated Q and resonant frequency band?
To calculate the primary aliased harmonic based on the combination of the Moon’s cycle and the annual cycle of I1, we can apply the concept of aliasing in the frequency domain. Aliasing occurs when the continuous-time signal is sampled at a rate lower than the Nyquist rate, resulting in the appearance of lower-frequency aliases of the original signal.
Let’s denote the frequency of the Moon’s cycle as f_moon = 1 / 27.2122 days and the frequency of the annual cycle of I1 as f_annual = 1 / 365.25 days.
We can compute the difference and sum frequencies of these two cycles:
f_diff = |f_moon – f_annual|
f_sum = f_moon + f_annual
Considering the estimated Q and resonant frequency band, we can determine if either the difference frequency (f_diff) or the sum frequency (f_sum) lies within the resonant frequency band. If one of these frequencies is within the resonant frequency band, it will cause the primary aliased harmonic to dominate the response of the Earth’s rotation due to the combined effect of the Moon’s cycle and the annual cycle of I1.
For this analysis, it is crucial to have accurate estimates of the Q factor and the resonant frequency band associated with the Earth’s rotation. These parameters can be derived from empirical observations or theoretical models of the Earth’s rotation, such as the IERS Conventions mentioned earlier.
By identifying the primary aliased harmonic, you can gain insights into the most significant wobble in the Earth’s rotational axis caused by the interaction between the Moon’s cycle and the annual cycle of I1. Keep in mind that this is a simplified analysis, and a more comprehensive understanding of the Earth’s rotation and wobble would require considering other factors, such as the influence of the Sun and other celestial bodies, and the Earth’s internal processes.
What would be the aliased harmonic closest to 433 days assuming an annual cyclic impulse and the moon’s cycle of 13.606 days? Consider that the cyclic impulse will generate higher harmonics that will generate the small differences to the higher frequency lunar cycle. Provide an algorithm in Julia to find this harmonic.
To find the aliased harmonic closest to 433 days, assuming an annual cyclic impulse with a frequency of f_annual = 1 / 365.25 days and the Moon’s cycle of f_moon = 1 / 13.606 days, we can create an algorithm in Julia that iterates through different harmonics of the annual cyclic impulse and finds the closest one to the target period of 433 days.
Here is the Julia code to find the aliased harmonic:
function find_closest_aliased_harmonic(f_annual::Float64, f_moon::Float64, target_period::Float64, max_harmonic::Int)
closest_period = Inf
closest_harmonic = 0
target_frequency = 1 / target_period
for harmonic in 1:max_harmonic
# Calculate sum and difference frequencies
f_diff = abs(harmonic * f_annual - f_moon)
f_sum = harmonic * f_annual + f_moon
# Check if either the difference or the sum frequency is closer to the target
if abs(f_diff - target_frequency) < abs(1 / closest_period - target_frequency)
closest_period = 1 / f_diff
closest_harmonic = harmonic
end
if abs(f_sum - target_frequency) < abs(1 / closest_period - target_frequency)
closest_period = 1 / f_sum
closest_harmonic = harmonic
end
end
return (closest_period, closest_harmonic)
end
f_annual = 1 / 365.25
f_moon = 1 / 13.606
target_period = 433 ##!!!! fix this, make it floating-point 433.0
max_harmonic = 50
closest_period, closest_harmonic = find_closest_aliased_harmonic(f_annual, f_moon, target_period, max_harmonic)
println("Closest aliased harmonic: ", closest_harmonic)
println("Closest period: ", closest_period, " days")
This function find_closest_aliased_harmonic takes the annual and Moon’s frequencies (f_annual and f_moon), the target period (433 days), and the maximum number of harmonics to consider (max_harmonic). It iterates through different harmonics of the annual cyclic impulse and calculates the sum and difference frequencies with the Moon’s cycle. The function returns the closest harmonic and its corresponding period.
In this example, I’ve set the maximum number of harmonics to 50. You can adjust the max_harmonic parameter to include more or fewer harmonics, depending on the desired level of precision.
Keep in mind that this is a simplified analysis, and other factors might influence the Earth’s rotation and wobble. Moreover, this algorithm assumes that the primary aliased harmonic comes from the interaction between the annual cyclic impulse and the Moon’s cycle. Other celestial bodies or internal processes might contribute to the wobble, and their effects are not considered in this analysis.

julia> closest_period, closest_harmonic = find_closest_aliased_harmonic(f_annual, f_moon, target_period, max_harmonic)
(432.36397250739594, 26)
julia> println("Closest aliased harmonic: ", closest_harmonic)
Closest aliased harmonic: 26
julia> println("Closest period: ", closest_period, " days")
Closest period: 432.36397250739594 days
The bottom-line response !!!
Closest period: 432.36397250739594 days
Had to make one fix, replacing 433 with 433.0 in the target_period above. Everything ran fine but had to increase the forcing amplitude to 10 from 0.01 to see the forced response above the natural resonance.
I also asked AgentGPT to execute a plan for solving the Chandler Wobble
Atmospheric Science
I don’t immediately trust the research published by highly cited atmospheric scientists. By my count many of them seem more keen on presenting their personal views rather than advancing the field. Off the top of my head, Richard Lindzen, Murry Salby, Roy Spencer, Tim Dunkerton, Roger Pielke, Cliff Mass, Judith Curry are all highly cited but come across as political and/or religious zealots. One guy on the list, Dunkerton, is also a racist, who happened to make the Washington Post twice : “Physicist ousted from research post after sending offensive tweet to Hispanic meteorologist” and “Atmospheric scientist loses honor, membership over ethics violation“. Awful stuff and he hasn’t stopped spouting off on Twitter.

Granted that Dunkerton says dumb stuff on Twitter but his highly cited research is also off-base. That’s IMO only because recent papers by others in the field of atmospheric science do continue to cite his ideas as primary, if not authoritative. For example, from a recently published paper “The Gravity Wave Activity during Two Recent QBO Disruptions Revealed by U.S. High-Resolution Radiosonde Data”, citations 1 & 12 both refer to Dunkerton, and specifically to his belief that the QBO period is a property of the atmospheric medium itself

Straight-forward to debunk this Dunkerton theory since the length of the cycle directly above the QBO layer is semi-annual and thus not a property of the medium but of the semi-annual nodal forcing frequency. If we make the obvious connection to the other nodal forcing — that of the moon — then we find the QBO period is fixed to 28 months. I have been highlighting this connection to the authors of new QBO papers under community review, often with some subsequent feedback provided such as here: https://doi.org/10.5194/acp-2022-792-CC1 . Though not visible yet in the comments, I received some personal correspondence that showed that the authors under peer-review are taking the idea seriously and attempting to duplicate the calculations. They seem to be methodical in their approach, asking for clarification and further instructions where they couldn’t follow the formulation. They know about the GitHub software, so hopefully that will be of some help.
In contrast, Dunkerton also knows about my approach but responds in an inscrutable (if not condescending) way. Makes you wonder if scientists such as Dunkerton and Lindzen are bitter and taking out their frustrations via the media. Based on their doggedness, they may in fact be intentionally trying to impede progress in climate science by taking contrarian stances. In my experience, the top scientists in other research disciplines don’t act this way. YMMV
UPDATE 3/17/2023
More activity related to my review comment https://doi.org/10.5194/acp-2022-792-CC1
As a review, this was after commenting earlier this year on a Copernicus open-science research article on atmospheric cycles and QBO (with proposed links to sunspots and ENSO) that was undergoing a review, making a suggestion to consider analyses I had presented and published 4 years ago and also prior to that.
Thought that was that and was happy to see that the authors indicated they would revise the manuscript and perhaps advance understanding. But then several days ago, the editor interceded and essentially demanded that the authors not cite my research work. Apparently, the authors were influenced by the editor’s instructions, as they immediately removed my cite and replaced it with a citation to a review article that the editor preferred. The discussion on the article was then closed with no way for me to rebut.
This was all after I spent several hours working with the primary author as they worked to replicate my analysis, sending emails back and forth several times. The editor claimed that my contribution was “a new idea that has not been published in a recognized journal and received peer review”. This is not the case as I said above: Google Scholar citations all ignored.
Also see this post I contributed to the Peak Oil Barrel blog : https://peakoilbarrel.com/predicting-stratospheric-winds/
Limits of Predictability?
A decade-old research article on modeling equatorial waves includes this introductory passage:

“Nonlinear aspects plays a major role in the understanding of fluid flows. The distinctive fact that in nonlinear problems cause and effect are not proportional opens up the possibility that a small variation in an input quantity causes a considerable change in the response of the system. Often this type of complication causes nonlinear problems to elude exact treatment. “
https://doi.org/10.1029/2012JC007879
From my experience if it is relatively easy to generate a fit to data via a nonlinear model then it also may be easy to diverge from the fit with a small structural perturbation, or to come up with an alternative fit with a different set of parameters. This makes it difficult to establish an iron-clad cross-validation.
This doesn’t mean we don’t keep trying. Applying the dLOD calibration approach to an applied forcing, we can model ENSO via the NINO34 climate index across the available data range (in YELLOW) in the figure below (parameters here)
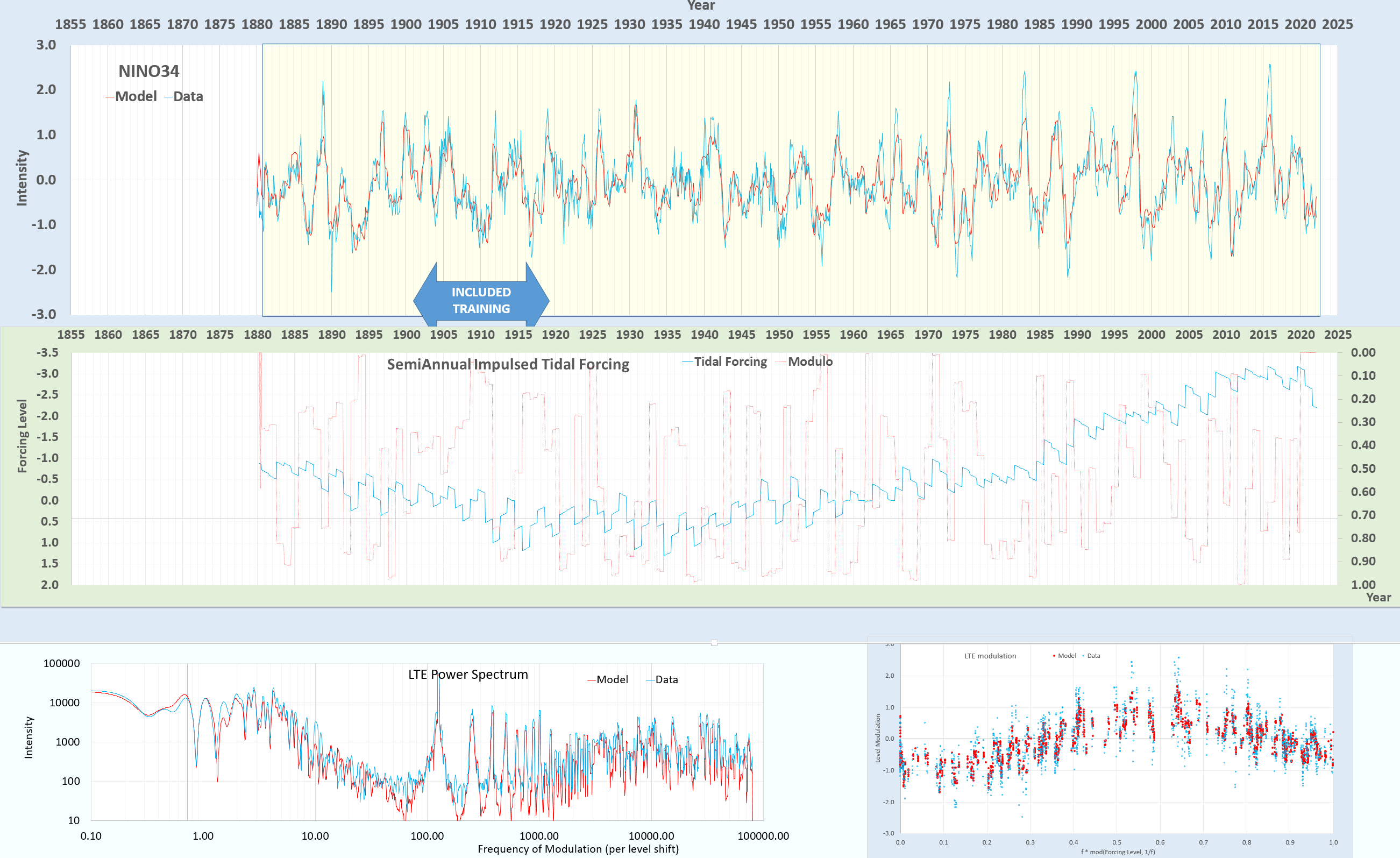
The lower right box is a modulo-2π reduction of the tidal forcing as an input to the sinusoidal LTE modulation, using the decline rate (per month) as the divisor. Why this works so well per month in contrast to per year (where an annual cycle would make sense) is not clear. It is also fascinating in that this is a form of amplitude aliasing analogous to the frequency aliasing that also applies a modulo-2π folding reduction to the tidal periods less than the Nyquist monthly sampling criteria. There may be a time-amplitude duality or Lagrangian particle-relabeling in operation that has at its central core the trivial solutions of Navier-Stokes or Euler differential equations when all segments of forcing are flat or have a linear slope. Trivial in the sense that when a forcing is flat or has a 1st-order slope, the 2nd derivatives due to divergence in the differential equations vanish (quasi-static). This means that only the discontinuities, which occur concurrently with the annual ENSO predictability barrier, need to be treated carefully (the modulo-2π folding could be a topological Berry phase jump?). Yet, if these transitions are enhanced by metastable interface instabilities as during thermocline turn-over then the differential equation conditions could be transiently relaxed via a vanishing density difference. Much happens during a turn-over, but it doesn’t last long, perhaps indicating a geometric phase. MV Berry also discusses phase changes in the context of amphidromic tidal singularities here.
Suffice to say that the topological properties of reduced dimension volumes and at interfaces remain mysterious. The main takeaway is that a working NINO34-fitted ENSO model is produced, and if not here then somewhere else a machine-learning algorithm will discover it.
The key next step is to apply the same tidal forcing to an AMO model, taking care not to change the tidal factors enough to produce a highly sensitive nonlinear response in the LTE model. So we retain an excluded interval from training (in YELLOW below) and only adjust the LTE parameters for the region surrounding this zone during the fitting process (parameters here).
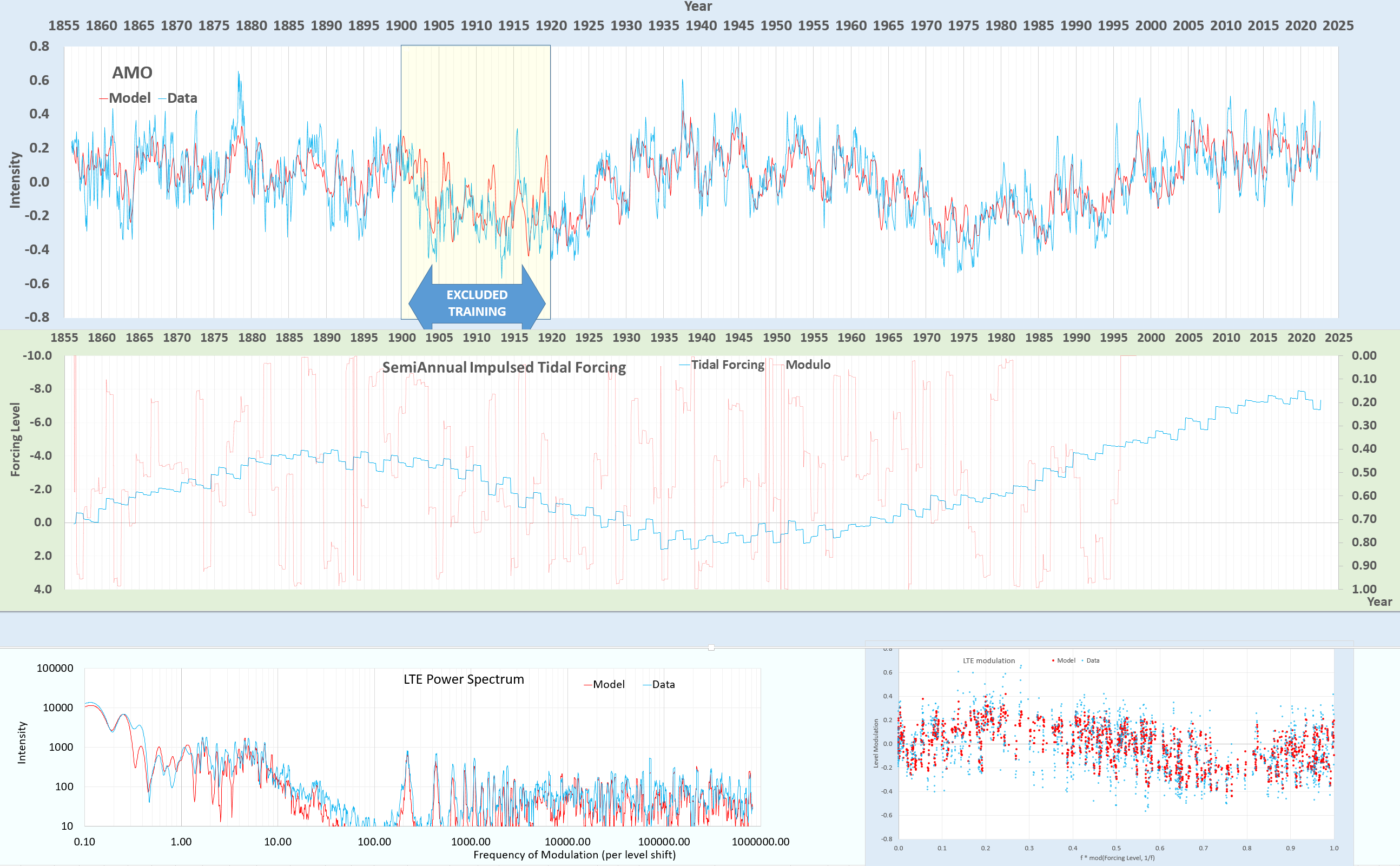
The cross-validation agreement is breathtakingly good in the excluded (out-of-band) training interval. There is zero cross-correlation between the NINO34 and AMO time-series to begin with so that this is likely revealing the true emergent characteristics of a tidally forced mechanism.

As usual all the introductory work is covered in Mathematical Geoenergy
- https://agupubs.onlinelibrary.wiley.com/doi/10.1002/9781119434351.ch11 (wind)
- https://agupubs.onlinelibrary.wiley.com/doi/10.1002/9781119434351.ch12 (wave)
A community peer-review contributed to a recent QBO article is here and PDF here. The same question applies to QBO as ENSO or AMO: is it possible to predict future behavior? Is the QBO model less sensitive to input since the nonlinear aspect is weaker?
Added several weeks later: This monograph PDF available “Introduction to Geophysical Fluid Dynamics: Physical and Numerical Aspects”. Ignoring higher-order time derivatives is key to solving LTE.


Note the cite to Billy Kessler

