A decade-old research article on modeling equatorial waves includes this introductory passage:

“Nonlinear aspects plays a major role in the understanding of fluid flows. The distinctive fact that in nonlinear problems cause and effect are not proportional opens up the possibility that a small variation in an input quantity causes a considerable change in the response of the system. Often this type of complication causes nonlinear problems to elude exact treatment. “
https://doi.org/10.1029/2012JC007879
From my experience if it is relatively easy to generate a fit to data via a nonlinear model then it also may be easy to diverge from the fit with a small structural perturbation, or to come up with an alternative fit with a different set of parameters. This makes it difficult to establish an iron-clad cross-validation.
This doesn’t mean we don’t keep trying. Applying the dLOD calibration approach to an applied forcing, we can model ENSO via the NINO34 climate index across the available data range (in YELLOW) in the figure below (parameters here)
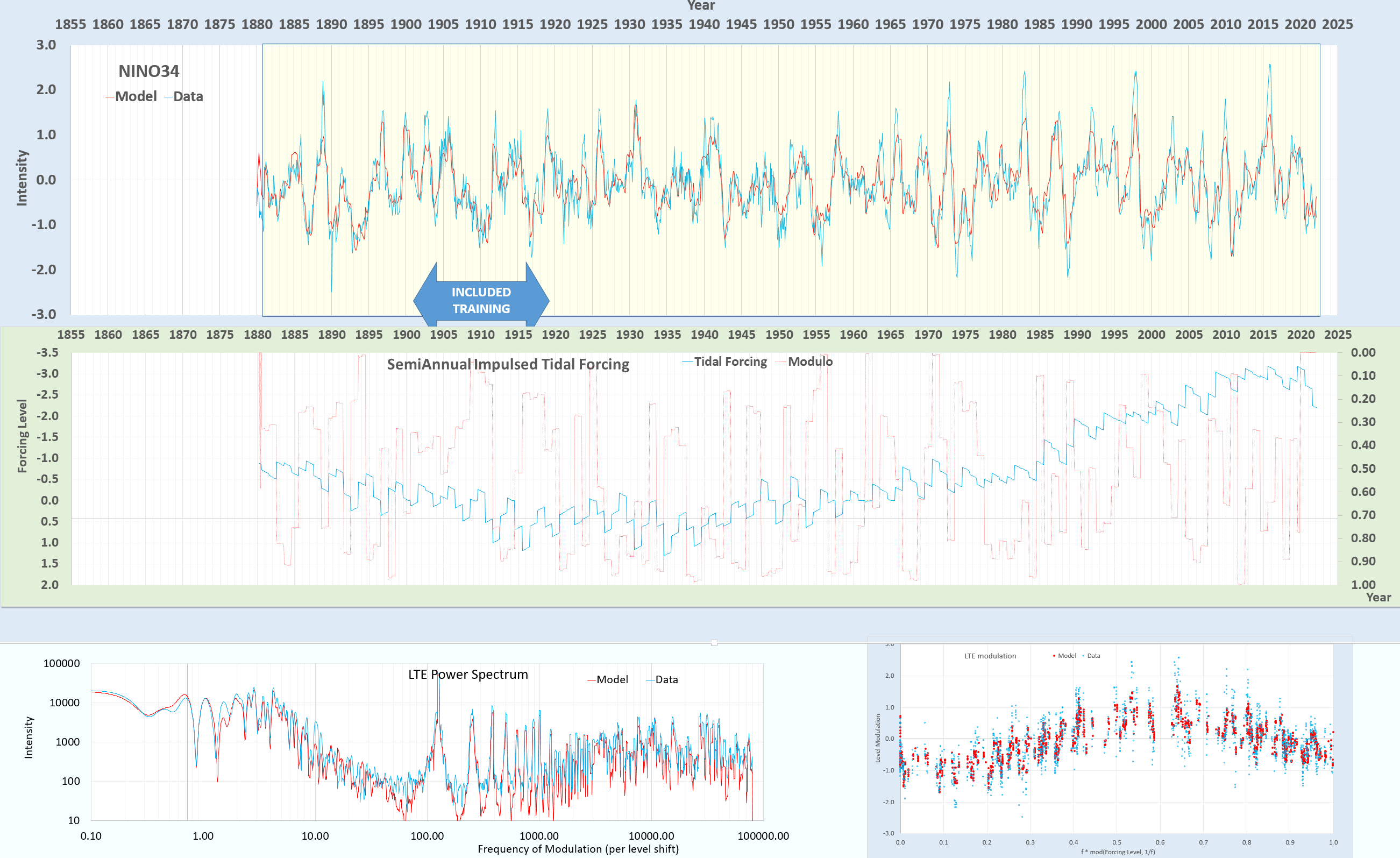
The lower right box is a modulo-2π reduction of the tidal forcing as an input to the sinusoidal LTE modulation, using the decline rate (per month) as the divisor. Why this works so well per month in contrast to per year (where an annual cycle would make sense) is not clear. It is also fascinating in that this is a form of amplitude aliasing analogous to the frequency aliasing that also applies a modulo-2π folding reduction to the tidal periods less than the Nyquist monthly sampling criteria. There may be a time-amplitude duality or Lagrangian particle-relabeling in operation that has at its central core the trivial solutions of Navier-Stokes or Euler differential equations when all segments of forcing are flat or have a linear slope. Trivial in the sense that when a forcing is flat or has a 1st-order slope, the 2nd derivatives due to divergence in the differential equations vanish (quasi-static). This means that only the discontinuities, which occur concurrently with the annual ENSO predictability barrier, need to be treated carefully (the modulo-2π folding could be a topological Berry phase jump?). Yet, if these transitions are enhanced by metastable interface instabilities as during thermocline turn-over then the differential equation conditions could be transiently relaxed via a vanishing density difference. Much happens during a turn-over, but it doesn’t last long, perhaps indicating a geometric phase. MV Berry also discusses phase changes in the context of amphidromic tidal singularities here.
Suffice to say that the topological properties of reduced dimension volumes and at interfaces remain mysterious. The main takeaway is that a working NINO34-fitted ENSO model is produced, and if not here then somewhere else a machine-learning algorithm will discover it.
The key next step is to apply the same tidal forcing to an AMO model, taking care not to change the tidal factors enough to produce a highly sensitive nonlinear response in the LTE model. So we retain an excluded interval from training (in YELLOW below) and only adjust the LTE parameters for the region surrounding this zone during the fitting process (parameters here).
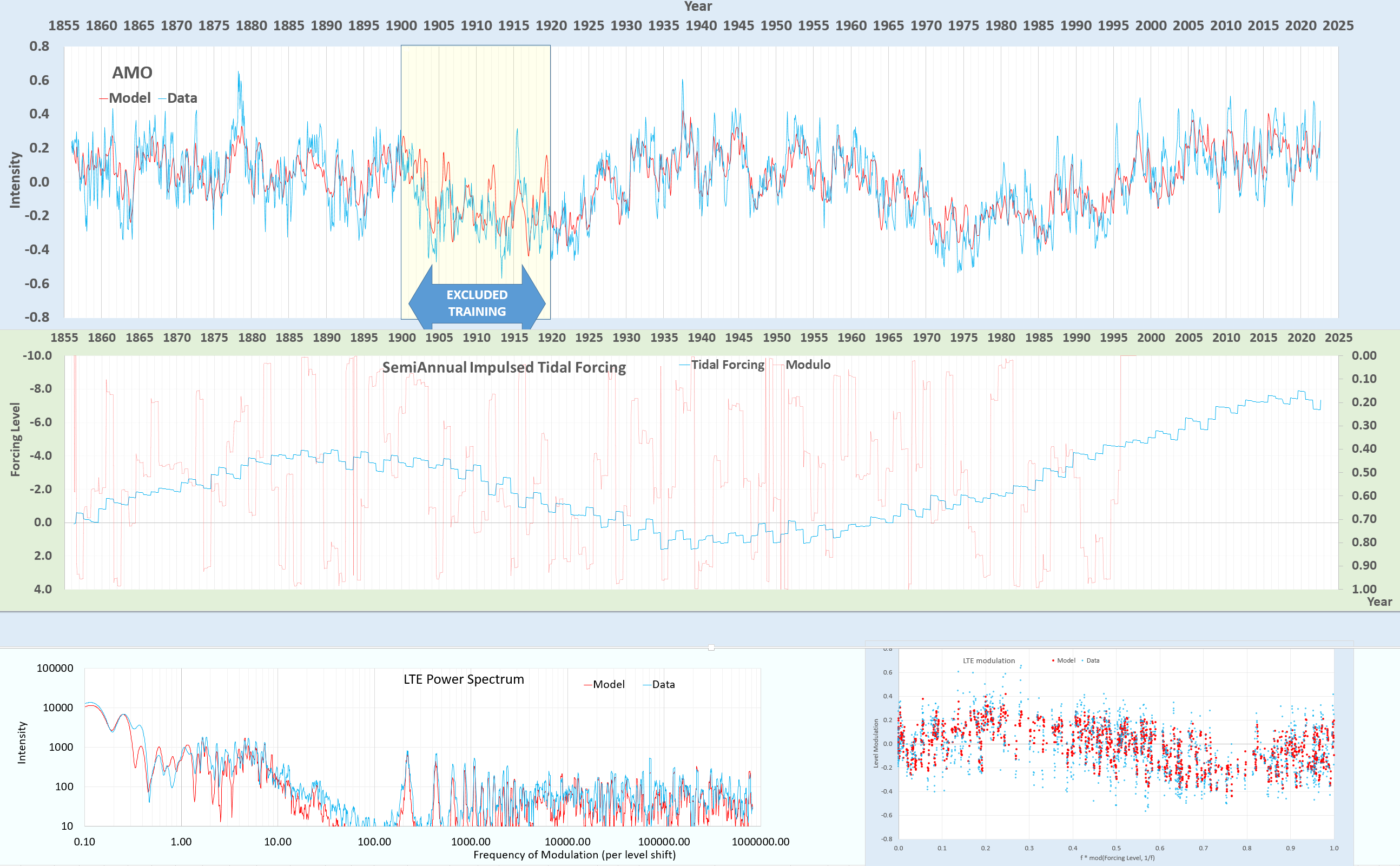
The cross-validation agreement is breathtakingly good in the excluded (out-of-band) training interval. There is zero cross-correlation between the NINO34 and AMO time-series to begin with so that this is likely revealing the true emergent characteristics of a tidally forced mechanism.

As usual all the introductory work is covered in Mathematical Geoenergy
- https://agupubs.onlinelibrary.wiley.com/doi/10.1002/9781119434351.ch11 (wind)
- https://agupubs.onlinelibrary.wiley.com/doi/10.1002/9781119434351.ch12 (wave)
A community peer-review contributed to a recent QBO article is here and PDF here. The same question applies to QBO as ENSO or AMO: is it possible to predict future behavior? Is the QBO model less sensitive to input since the nonlinear aspect is weaker?
Added several weeks later: This monograph PDF available “Introduction to Geophysical Fluid Dynamics: Physical and Numerical Aspects”. Ignoring higher-order time derivatives is key to solving LTE.


Note the cite to Billy Kessler

The limits of predictability: a philosophical perspective from an above average Joe. (hubris intended). I cannot accurately predict anything until I understand everything.
I appreciate the way you continue to push the boundaries of understanding.
Thanks Pukite
LikeLike
Superoscillations and the quantum potential, MV Berry
https://iopscience.iop.org/article/10.1088/1361-6404/abc5fd/pdf
A superoscillation is like a delta-function or step change
https://iopscience.iop.org/article/10.1088/1367-2630/ac2bd7/pdf
Semiclassical superoscillations: interference, evanescence, post-WKB, MV Berry
Sean Carroll podcast with M.M. https://www.preposterousuniverse.com/podcast/2019/09/23/65-michael-mann-on-why-our-climate-is-changing-and-how-we-know/
Roadmap on superoscillations, Berry, Aharanov, others
https://iopscience.iop.org/article/10.1088/2040-8986/ab0191/meta
interferometric phase
https://www.sciencedirect.com/science/article/pii/S0375960122006351
Generalizations of Berry phase and differentiation of purified state and thermal vacuum of mixed states
LikeLike
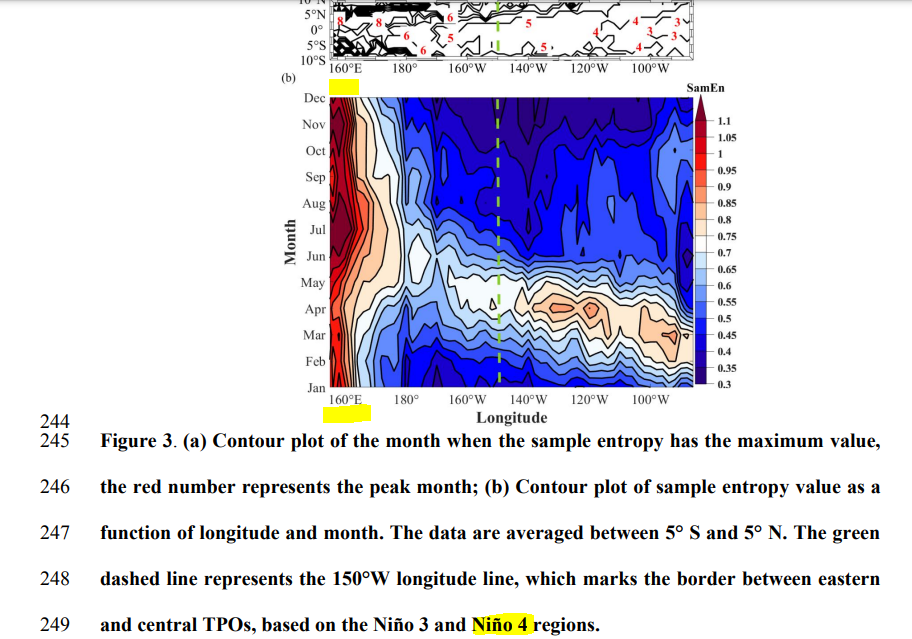
Implications from this paper — use NINO4 when possible?
A Nonlinear Cause for the seasonal Predictability Barrier of SST
anomaly in the 2 tropical Pacific
Click to access 8b1ed053f271d2322cadb0c682a8386f.pdf
The Sample Entropy increases when there is more self-similarity within a time-series
LikeLike