Month: September 2017

ENSO tidal forcing validated by LOD data

/ Paul Pukite (@whut) / 21 Comments

This is a straightforward validation of the forcing used on the lunar-driven ENSO model.

The paper by Chao et al [1] provides a comprehensive spectral analysis of the earth’s length of day (LOD) variations using both a wavelet analysis and a power spectrum analysis. The wavelet analysis provides insight into the richness of the LOD cyclic variations (c.f. the Chao ref 6 in a recent post) :

Both the wavelet and the power spectrum (below) show the 6-year Fourier component that appears in the ENSO model as a mixed tidal forcing.

The original premise is that the change in LOD via the equivalent angular momentum change will impart a forcing on the Pacific ocean thermocline as per a reduced-gravity model:

Taken from presentation for ref [2]

Calculating a spectral analysis of the best fit ENSO model forcing, note that all of the model peaks (in RED) match those found by Chao et al in their ΔLOD analysis :

There are additional peaks not found by Chao but those are reduced in magnitude, as can be inferred from the log (i.e. dB) scale. If these actually exist in the Chao spectrum, they may be buried in the background noise.  Also, the missing Sa and Ssa peaks are the seasonal LOD variations that are taken into account separately by the model, as most ENSO data sets are typically filtered to remove seasonal data.

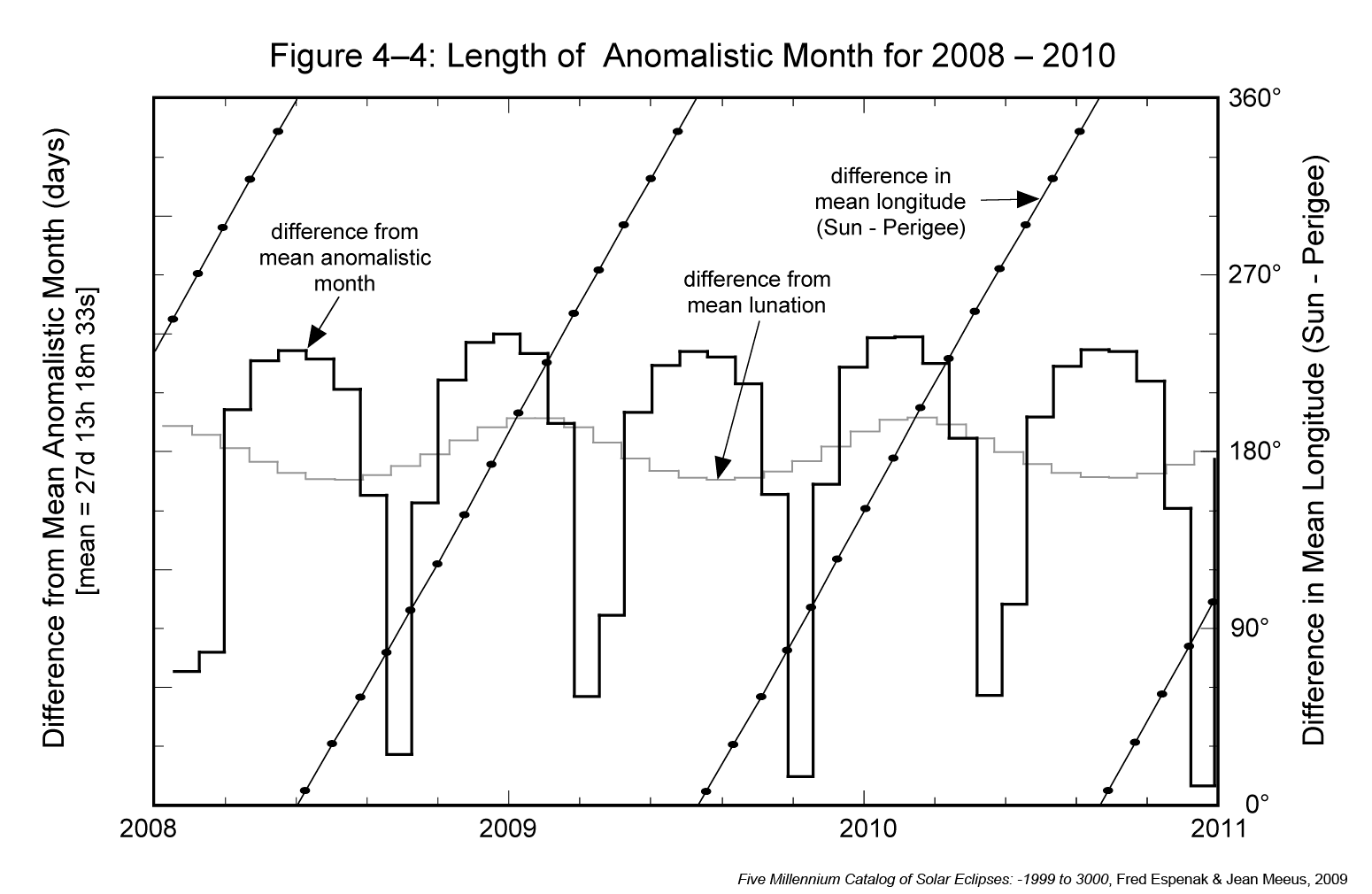
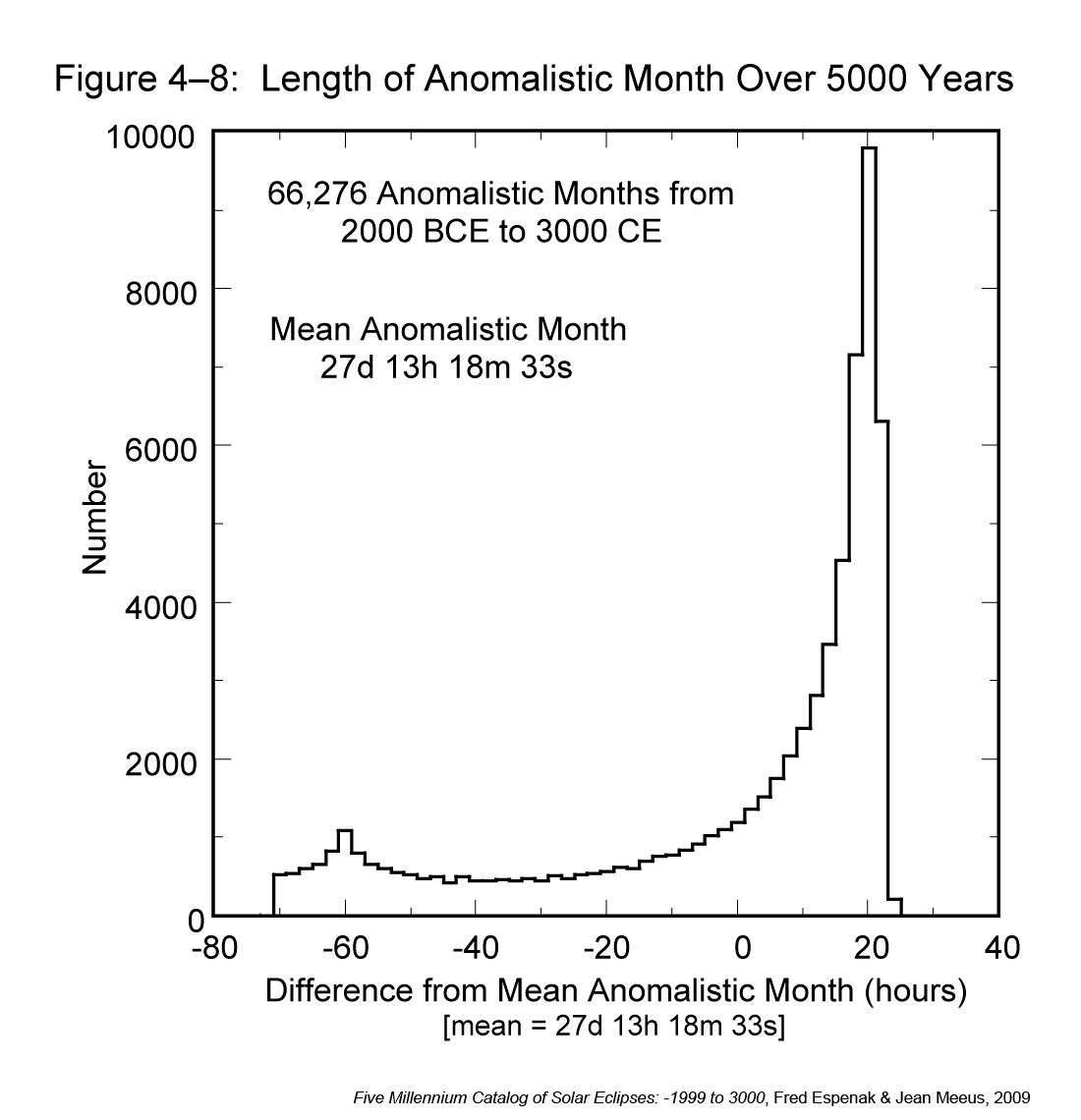
The tidal constituents shown above in the Chao power spectra are defined in the following Doodson table [3]. Chao likely is unable to discriminate the tropical values from the draconic and anomalistic values, being so close in value. On the other hand, the ENSO model needs to know these values precisely.  Each of the primary Mm, Mf, Mtm, and Mqm and satellite Msm, Msf, Mstm, Msqm factors align with the first 4 harmonics of the mixed nonlinear ENSO model with the 2nd order satellites arising from the anomalistic correction.

Tidal constituent coefficients taken from ref [3]

This is an excellent validation test because this particular LOD power spectrum has not been used previously in the ENSO model fitting process. If the peaks did not match up, then the original premise for LOD forcing would need to be reconsidered.

 

References

[1] B. F. Chao, W. Chung, Z. Shih, and Y. Hsieh, “Earth’s rotation variations: a wavelet analysis,” Terra Nova, vol. 26, no. 4, pp. 260–264, 2014.

[2] A. Capotondi, “El Niño–Southern Oscillation ocean dynamics: Simulation by coupled general circulation models,” Climate Dynamics: Why Does Climate Vary?, pp. 105–122, 2013.

[3] D. D. McCarthy (ed.): IERS Conventions (1996) (IERS Technical Note No. 21) :
Chapter 6

Earthquakes, tides, and tsunami prediction

/ Paul Pukite (@whut) / 6 Comments

I’ve been wanting to try this for awhile — to see if the solver setup used for fitting to ENSO would work for conventional tidal analysis.  The following post demonstrates that if you give it the recommended tidal parameters and let the solver will grind away, it will eventually find the best fitting amplitudes and phases for each parameter.

The context for this analysis is an excellent survey paper on tsunami detection and how it relates to tidal prediction:

S. Consoli, D. R. Recupero, and V. Zavarella, “A survey on tidal analysis and forecasting methods for Tsunami detection,” J. Tsunami Soc. Int.
33 (1), 1–56.

The question the survey paper addresses is whether we can one use knowledge of tides to deconvolute and isolate a tsunami signal from the underlying tidal sea-level-height (SLH) signal. The practical application paper cites the survey paper above:

Percival, Donald B., et al. “Detiding DART® buoy data for real-time extraction of source coefficients for operational tsunami forecasting.” Pure and Applied Geophysics 172.6 (2015): 1653-1678.

This is what the raw buoy SLH signal looks like, with the tsunami impulse shown at the end as a bolded line:

After removing the tidal signals with various approaches described by Consoli et al, the isolated tsunami impulse response (due to the 2011 Tohoku earthquake) appears as:

As noted in the caption, the simplest harmonic analysis was done with 6 constituent tidal parameters.

As a comparison, the ENSO solver was loaded with the same tidal waveform (after digitizing the plot) along with 4 major tidal parameters and 4 minor parameters to be optimized. The solver’s goal was to maximize the correlation coefficient between the model and the tidal data.

q

The yellow region is training which reached almost a 0.99 correlation coefficient, with the validation region to the right reaching 0.92.

This is the complex Fourier spectrum (which is much less busy than the ENSO spectra):

qf

The set of constituent coefficients we use is from the Wikipedia page where we need the periods only. Of the following 5 principal tidal constituents, only N2 is a minor factor in this case study.

In practice, multiple linear regression would provide faster results for tidal analysis as the constituents add linearly (see the CSALT model). In contrast, for ENSO there are several nonlinear steps required that precludes a quick regression solution.  Yet, this tidal analysis test shows how effective and precise a solution the solver supplies.

The entire analysis only took an evening of work, in comparison to the difficulty of dealing with ENSO data, which is much more noisy than the clean tidal data.  Moreover, the parameters for conventional tidal analysis stress the synodic/tropical/sidereal constituents — unfortunately, these are of little consequence for ENSO analysis, which requires the draconic and anomalistic parameters and the essential correction factors. The synodic tide is the red herring for the unwary when dealing with global phenomena such as ENSO, QBO, and LOD. The best way to think about it is that the synodic cycle impacts locally and most immediately, whereas the anomalistic and draconic cycles have global and more cumulative impacts.

The 6-year oscillation in Length-of-Day

/ Paul Pukite (@whut) / Leave a comment

A somewhat hidden cyclic variation in the length-of-day (LOD) in the earth’s rotation, of between 6 and 7 years, was first reported in Ref [1] and analyzed in Ref [2]. Later studies further refined this period [3,4,5] closer to 6 years.

Change in detected LOD follows a ~6-yr cycle, from Ref [3]

It’s well known that the moon’s gravitational pull contributes to changes in LOD [6]. Here is the set of lunar cycles that are applied as a forcing to the ENSO model using LOD as calibration.
Continue reading →

100 years of Walter Munk … and the role of lunar tides in ocean circulation

/ Paul Pukite (@whut) / 1 Comment

A piece celebrating the 100 year birthday of Walter Munk.

” … a body of work that is wide-ranging and tremendously practical. His decades of discoveries have shaped what humanity knows about the nature of waves, currents, tides, global ocean circulation and deep-sea drilling. “

Which raises the interesting issue of the largely ignored paper by Munk’s colleague Carl Wunsch and his paper “Moon, tides, and climate” in the 15 June 2000 issue of Nature.

“But Munk and I concluded that about half of the power required to return the deep waters to the surface was coming from mixing driven primarily by dissipation of tidal energy — principally lunar, but with a minor solar component — in the deep ocean (Fig. 1).”

What’s interesting about this is that there are three scales and modes at which tidal forces can have an impact on the ocean circulation

  1. Conventional ocean tides
    (provably forced by moon + sun, with tiny but measurable amount by wind)
  2. Thermocline sloshing, i.e. ENSO, as per Clarke [1]
    (believed to be forced by wind)
  3. Deep ocean mixing described by Wunsch & Munk  [2]
    (forced by mix of moon and wind)

This is what I find perplexing. For some reason tidal energy is excluded from contributing to #2 even though the periods of the ENSO cycle are precisely commensurate with the lunar fortnightly and monthly long periods.

The analogy is like saying that both rain and hail are caused by coalescence of water in the atmosphere, but snow isn’t. I know that’s an extreme analogy, but trying to get wide acknowledgment or to even get this lunar mode considered for #2  will take a huge amount of effort.  It would be interesting to ask Munk what he thinks of the ENSO lunar forcing model.

BTW, that paper by Wunsch suffered from what I considered an ill-advised attempt at humor. This is Fig.1 that Wunsch referred to in the excerpt above:

There was no content, only a lame joke worthy of Yakov Smirnoff.  That was not a good decision if you wanted other scientists to take the article seriously, IMO.

The joke was repeated here by Munk and Wunsh, in a slight reworking. This may have been a precursor draft to the Nature article, of which Munk did not appear as a co-author.

Conclusion

As per Munk and Wunsch on the influence of the moon on the pelagic (open ocean) zone:

“Our very tentative conclusions are that l) tidal dissipation plays a dominant role in pelagic mixing processes”

References

[1] A. J. Clarke, S. Van Gorder, and G. Colantuono, “Wind stress curl and ENSO discharge/recharge in the equatorial Pacific,” Journal of physical oceanography, vol. 37, no. 4, pp. 1077–1091, 2007

[2] Munk, W. & Wunsch, C. Deep-Sea Res. 45, 1976–2009 (1998).

 

Limits to Goodness of Fit

/ Paul Pukite (@whut) / 2 Comments

Based on a comparison of local interval correlations between the NINO34 and SOI indices, there probably is a limit to how well a model can be fit to ENSO.  The lower chart displays a 4-year-windowed correlation coefficient (in RED) between the two indices (shown in upper chart):

Note that in the interval starting at 1930, the correlation is poor for about 7 years.

Next note that the ENSO model fit shows a poor correlation to the NINO34 data in nearly the same intervals (shown as dotted GREEN). This is an odd situation but potentially revealing. The fact that both the ENSO model and SOI don’t match the NINO34 index over the same intervals, suggests that the model may match SOI better than it does NINO34.  Yet, because of the excessive noise in SOI, this is difficult to verify.

But more fundamentally, why would NINO34 not match SOI in these particular intervals? These regions do seem to be ENSO-neutral, not close to El Nino or La Nina episodes.  Some also seem to occupy regions of faster, noisy fluctuations in the index.

It could be that the ENSO lunar tidal model is revealing the true nature of the ENSO dynamics, and these noisier, neutral regions are reflecting some other behavior (such as amplitude folding) — but since they also appear to be obscured by noise, it makes it difficult to unearth.

 

The paper by Zajączkowska[1] also applies a local correlation to compare the lunar tidal cycles to plant growth dynamics. There’s a treasure trove of recent research on this topic.

References

Second-Order Effects in the ENSO Model

/ Paul Pukite (@whut) / 4 Comments

For ocean tidal predictions, once an agreement is reached on the essential lunisolar terms, then the second-order terms are refined. Early in the last century Doodson catalogued most of these terms:

“Since the mid-twentieth century further analysis has generated many more terms than Doodson’s 388. About 62 constituents are of sufficient size to be considered for possible use in marine tide prediction, but sometimes many fewer can predict tides to useful accuracy.”

That’s possibly the stage we have reached in the ENSO model.  There are two primary terms for lunar forcing (the Draconic and Anomalistic) cycles, that when mixed with the annual and biannual cycles, will reproduce the essential ENSO behavior.  The second-order effects are the  modulation of these two lunar cycles with the Tropical/Synodic cycle.  This is most apparent in the modification of the Anomalistic cycle. Although not as important as in the calculation of the Total Solar Eclipse times, the perturbation is critical to validating the ENSO model and to eventually using it to make predictions.

The variation in the Anomalistic period is described at the NASA Goddard eclipse page. They provide two views of the variation, a time-domain view and a histogram view.

Time domain view Histogram view

Since NASA Goddard doesn’t provide an analytical form for this variation, we can see if the ENSO Model solver can effectively match it via a best-fit search to the ENSO data. This is truly an indirect method.

First we start with a parametric approximation to the variation, described by a pair of successive frequency modulated (and full-wave rectified) terms that incorporate the Tropical-modified term, wm. The Anomalistic term is wa.

COS(wa*t+pa+c_1*ABS(SIN(wm*t+k_1*ABS(SIN(wm*t+k_2))+c_2)))

cos(omega_a t+phi_a+c_1 cdot |sin(omega_m t+k_1 cdot |sin(omega_m t+k_2)|+c_2)|)

This can generate the cusped behavior observed, but the terms pa, c_1, c_2, k_1, and k_2 need to be adjusted to align to the NASA model. The solver will try to do this indirectly by fitting to the 1880-1950 ENSO interval.

Plotting in RED the Anomalistic time series and the histogram of frequencies embedded in the ENSO waveform, we get:

Time domain view of model Histogram view of model

This captures the histogram view quite well, and the time-domain view roughly (in other cases it gives a better cusped fit).  The histogram view is arguably more important as it describes the frequency variation over a much wider interval than the 3-year interval shown.

What would be even more effective is to find the correct analytical representation of the Anomalistic frequency variation and then plug that directly into the ENSO model. That would provide another constraint to the solver, as it wouldn’t need to spend time optimizing for a known effect.

Yet as a validation step, the fact that the solver detects the shape required to match the variation is remarkable in itself. The solver is obviously searching for the forcing needed to produce the ENSO waveform observed, and happens to use the precise parameters that also describe the second-order Anomalistic behavior.  That could happen by accident but in that case there have been too many happy accidents already, i.e. period match, LOD match, Eclipse match, QBO match, etc.

Using Solar Eclipses to calibrate the ENSO Model

/ Paul Pukite (@whut) / 2 Comments

This is the forcing for the ENSO model, focusing on the non-mixed Draconic and Anomalistic cycles:

Note that the maximum excursions (perigee and declination excursion) align with the occurrence of total solar eclipses. These are the first three that I looked at, which includes the latest August 21 eclipse in the center chart.

There are about 90 more of these stretching back to 1880. The best way to fit the calibration is to take the negative excursions of the two lunar forcings and multiply these together, i.e. use the effective Draconic*Anomalistic amplitudes (also only take the fortnightly cycle of the Draconic, as eclipses occur during both the ascending and descending node crossings). The main fitting factors are the phases of the two lunar months.  To get the maximum alignment from the search solver, we maximize the sum of the effective amplitudes across the entire interval. This results in a phase difference between the two of about 0.74 radians based at the starting year of 1880 (i.e. year 0).

Continue reading →

The QBO anomaly of 2016 revisited

/ Paul Pukite (@whut) / 7 Comments

Remember the concern over the QBO anomaly/disruption during 2016?

Quite a few papers were written on the topic

  1. Newman, P. A., et al. “The anomalous change in the QBO in 2015–2016.” Geophysical Research Letters 43.16 (2016): 8791-8797.
    Newman, P. A., et al. “The Anomalous Change in the QBO in 2015-16.” AGU Fall Meeting Abstracts. 2016.
  2. Randel, W. J., and M. Park. “Anomalous QBO Behavior in 2016 Observed in Tropical Stratospheric Temperatures and Ozone.” AGU Fall Meeting Abstracts. 2016.
  3. Dunkerton, Timothy J. “The quasi‐biennial oscillation of 2015–2016: Hiccup or death spiral?.” Geophysical Research Letters 43.19 (2016).
  4. Tweedy, O., et al. “Analysis of Trace Gases Response on the Anomalous Change in the QBO in 2015-2016.” AGU Fall Meeting Abstracts. 2016.
  5. Osprey, Scott M., et al. “An unexpected disruption of the atmospheric quasi-biennial oscillation.” Science 353.6306 (2016): 1424-1427.
According to the lunar forcing model of QBO, which was also presented at AGU last year, the peak in acceleration should have occurred at the time pointed to by the BLACK downward arrow in the figure below. This was in April of this year. The GREEN is the QBO 30 hPa acceleration data and the RED is the QBO model.

Note that the training region for the model is highlighted in YELLOW and is in the interval from 1978 to 1990. This was well in the past, yet it was able to pinpoint the sharp peak 27 years later.

The disruption in 2015-2016 shown with shaded black may have been a temporary forcing stimulus.  You can see that it obviously flipped the polarity with respect to the model. This will provoke a transient response in the DiffEq solution, which will then eventually die off.

The bottom-line is that the climate scientists who pointed out the anomaly were correct in that it was indeed a disruption, but this wasn’t necessarily because they understood why it occurred — but only that it didn’t fit a past pattern. It was good observational science, and so the papers were appropriate for publishing.  However, if you look at the QBO model against the data, you will see many similar temporary disruptions in the historical record. So it was definitely not some cataclysmic event as some had suggested. I think most scientists took a less hysterical view and simply pointed out the reversal in stratospheric winds was unusual.

I like to use this next figure as an example of how this may occur (found in the comment from last year). A local hurricane will temporarily impact the tidal displacement via a sea swell. You can see that in the middle of the trace below. On both sides of this spike, the tidal model is still in phase and so the stimulus is indeed transient while the underlying forcing remains invariant. For QBO, instead of a hurricane, the disruption could be caused by a SSW event. It also could be an unaccounted-for lunar forcing pulse not captured in the model. That’s probably worth more research.

As the QBO is still on a 28 month alignment, that means that the external stimulus — as with ENSO, likely the lunar tidal force — is providing the boundary condition synchronization.