Month: October 2019

Autocorrelation in Power Spectra, continued

/ Paul Pukite (@whut) / 8 Comments

This is a short comment pointing to an addition to a previous post https://geoenergymath.com/2019/02/16/autocorrelation-of-enso-power-spectrum/.

The context is looking for autocorrelations in the frequency domain of a time-series. Although not as common as performing autocorrelations in the time domain, it is equally as powerful.

The earlier idea was to look for harmonics in the periodicity of the ENSO signal, and the chart described in the post showed clear annual and higher harmonics in the time series. This was via a straightforward sliding autocorrelation in the power spectra.

As an additional technique, we can look for symmetric sidebands of the annual fundamental and harmonics frequencies by folding the spectra over about the annual frequency and performing a direct correlation calculation.

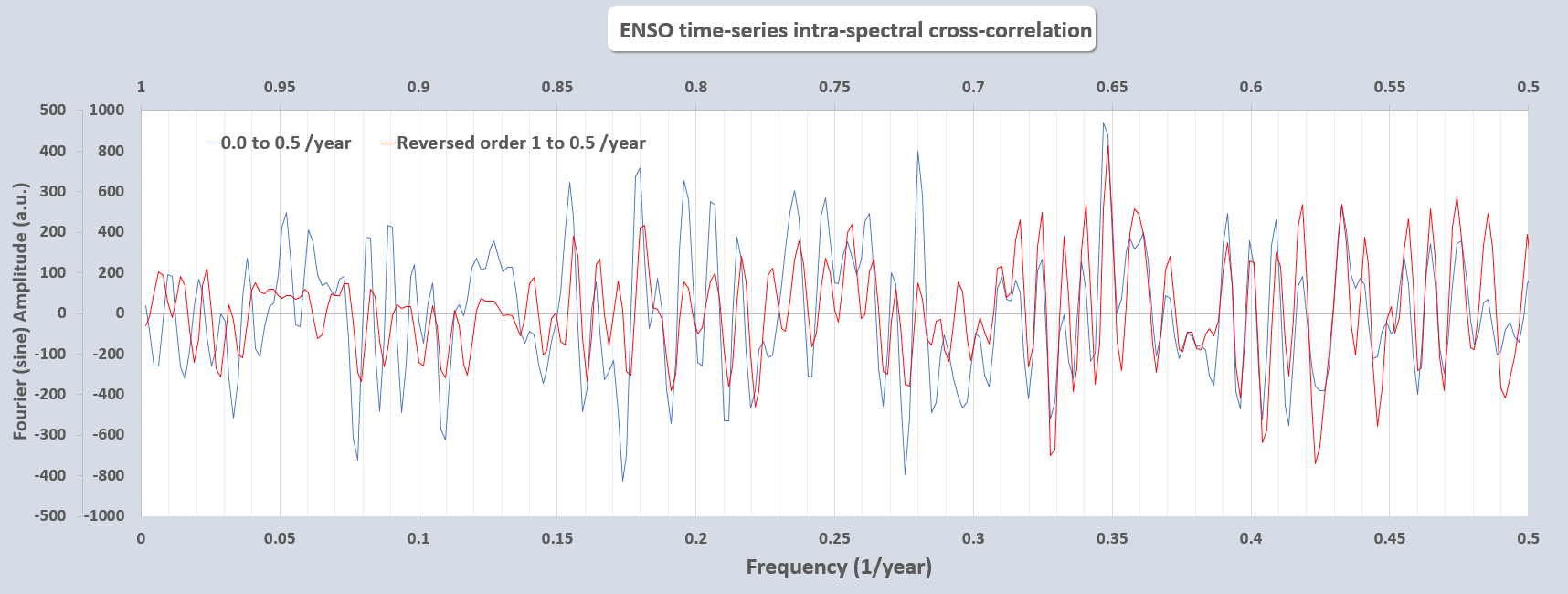
Lower x-axis is the lower sideband interval (blue) and
upper x-axis is the symmetric upper sideband interval (red) shown in reverse

This correlation is painfully obvious and is well beyond statistically significant in demonstrating that an annual impulse signal is modulating another much more complex forcing signal (likely of tidal origin). This is actually a well-known process known as a double-sideband suppressed carrier modulation, used most commonly in facilitating broadcast transmissions. As shown in the equations below, the modulation acts to completely suppress the carrier (i.e. annual) frequency.

Read the previous post for more detail on the approach.

Ordinarily, the demodulation is straightforward via a standard mixing approach, as the carrier signal is a much higher frequency than the informational signal, but since annual and long-period tides are of roughly similar periods, the demodulation will only complicate the spectrum. This is not a big deal as we need to fit the peaks via the LTE formulation in any case.

This is a new and novel finding and not to be found anywhere in the ENSO research literature. Why it hasn’t been uncovered yet is a bit of a mystery, but the fact that the annual signal is completely suppressed may be a hint. It may be that we need to understand why the dog didn’t bark.

Gregory (Scotland Yard detective): “Is there any other point to which you would wish to draw my attention?”
Holmes: “To the curious incident of the dog in the night-time.”
Gregory: “The dog did nothing in the night-time.”
Holmes: “That was the curious incident.”

— “The Adventure of Silver Blaze” by Sir Arthur Conan Doyle

If that is not the case, and this has been published elsewhere, will update this post.

Wind Energy Dispersion

/ Paul Pukite (@whut) / 2 Comments

In Chapter 11 of the book, we derive the distribution of wind speeds and show what role the concept of maximum entropy plays into the formulation. It’s a simple derivation and one that can be extended by layering more dispersion on the variability, in effect superposing more uncertainty on the Rayleigh or Weibull distribution that is typically used to quantify wind speed distribution. This is often referred to as superstatistics, first described by Beck, C., & Cohen, E. (2003) in Physica A: Statistical Mechanics and Its Applications, 322, 267–275.

A recent article uploaded to arXiv [1] gives an alternate treatment to the one we described. This follows Beck’s original approach more than our simplified formulation but each is an important contribution to understanding and applying the math of wind variability. The introduction to their article is valuable in providing a rationale for doing the analysis.

“Mitigating climate change demands a transition towards renewable electricity generation, with wind power being a particularly promising technology. Long periods either of high or of low wind therefore essentially define the necessary amount of storage to balance the power system. While the general statistics of wind velocities have been studied extensively, persistence (waiting) time statistics of wind is far from well understood. Here, we investigate the statistics of both high- and low-wind persistence. We find heavy tails and explain them as a superposition of different wind conditions, requiring q-exponential distributions instead of exponential distributions. Persistent wind conditions are not necessarily caused by stationary atmospheric circulation patterns nor by recurring individual weather types but may emerge as a combination of multiple weather types and circulation patterns. Understanding wind persistence statistically and synoptically, may help to ensure a reliable and economically feasible future energy system, which uses a high share of wind generation. “

[1]Weber, J. et al. “Wind Power Persistence is Governed by Superstatistics”. arXiv preprint arXiv:1810.06391 (2019).