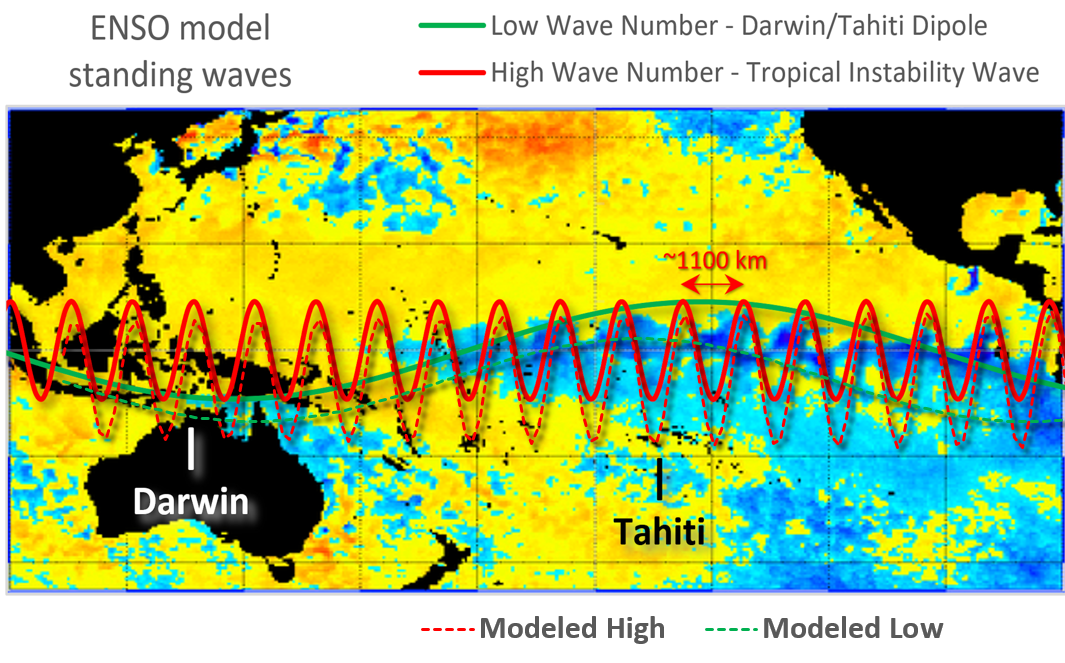
In Chapter 12 of the book, we present the hypothesis that tropical instability waves (TIW) of the equatorial Pacific are the higher wavenumber (and higher frequency) companion to the lower wavenumber ENSO (El Nino /Southern Oscillation) behavior. See Fig 1 below.

TIW wavetrains are also observed in the equatorial Atlantic so would be considered alongside the AMO there as the high wavenumber and low wavenumber pairing.

According to the Laplace’s Tidal Equation (LTE) model that we applied to ocean thermocline dynamics, TIW wavetrains originate from the higher-order solutions to the LTE differential equation. As with any waveguide containing standing-wave behaviors, the spatio-temporal solution allows for multiple wavelength/frequency combinations — in the case of LTE, it’s solved resulting in a linear dispersion relation, k ~ f. So for the Pacific ENSO + TIW pairing, the ratio is ~15:1, with the TIW wavelength ~15 times shorter than the ENSO standing wave (see Fig 1) and the TIW LTE amplitude modulation also 15 times the ENSO LTE modulation. This faster modulation is shown in the inset in the upper panel in Fig 2 below. The specific combination of slower and faster modulation provides the proper mix of harmonics to recreate the spikiness in the ENSO time-series.

As with any application of harmonics, the most important aspect is in modifying the shape (e.g. triangle, square, sawtooth) of the waveform and not in the overall period. Adding the higher-order modulation via the 15x TIW wavenumber is shown in Fig 3 below, with a clear enhancement of the sharpness in the overall fit by comparing the upper plot to the lower plot.

A recent paper titled “A simple theory for the modulation of tropical instability waves by ENSO and the annual cycle” [1] suggests a similar close relationship between ENSO and TIW. They refer to it as a simple model in that specific harmonics related to the ENSO cycle and annual cycle comprise the TIW wavetrain, which they empirically establish from an isolated TIW time-series. In contrast, in our model, the relation is determined by the nature of the LTE modulation. Fig 4 below shows our unfitted TIW model (extracted as the 15x factor) alongside the model from the Boucherel paper.

This is unfitted in the sense that the principal higher wavenumber solution derives only from a best fit of the LTE model to the NINO34/SOI time-series data — essentially the higher harmonics contribution of Fig 3. This has the byproduct of fitting the observed TIW as in Fig 4, thus creating the faster surface temperature cycles.

What is not called out by the Boucherel paper is that the TIW may actually amplify ENSO, whereas they show it having an opposite polarity relationship. That is dependent on where they are measuring the amplitude of the standing wave as shown in Fig 5 below. To investigate this further, it will be useful to have access to the complete set of data and reproduce their regression procedure to isolate the TIW component.

References

[1] Boucharel, J. and Jin, F.F., 2020. A simple theory for the modulation of tropical instability waves by ENSO and the annual cycle. Tellus A: Dynamic Meteorology and Oceanography, 72(1), pp.1-14.