In Chapter 12 of the book, we discuss tropical instability waves (TIW) of the equatorial Pacific as the higher wavenumber (and higher frequency) companion to the lower wavenumber ENSO (El Nino /Southern Oscillation) behavior. Sutherland et al have already published several papers this year that appear to add some valuable insight to the mathematical underpinnings to the fluid-mechanical relationship.
“It is estimated that globally 1 TW of power is transferred from the lunisolar tides to internal tides[1]. The action of the barotropic tide over bottom topography can generate vertically propagating beams near the source. While some fraction of that energy is dissipated in the near field (as observed, for example, near the Hawaiian Ridge [2]), most of the energy becomes manifest as low-mode internal tides in the far field where they may then propagate thousands of kilometers from the source [3]. An outstanding question asks how the energy from these waves ultimately cascades from large to small scale where it may be dissipated, thus closing this branch of the oceanic energy budget. Several possibilities have been explored, including dissipation when the internal tide interacts with rough bottom topography, with the continental slopes and shelves, and with mean flows and eddies (for a recent review, see MacKinnon et al. [4]). It has also been suggested that, away from topography and background flows, internal modes may be dissipated due to nonlinear wave-wave interactions including the case of triadic resonant instability (hereafter TRI), in which a pair of “sibling” waves grow out of the background noise field through resonant interactions with the “parent” wave”
see reference [2]
The idea is that a triad of waves of different frequencies and wavenumbers is required to efficiently exchange energies between the standing wave modes. This is expressed as the wavenumber relation K = Ka + Kb, where essentially the beat frequency of the two latter “sibling” waves Ka and Kb matches the fundamental frequency of the parent, K. This is similar to the relationship cited in our book due to Rajchenbach & Clamond [5] and described in an earlier post to support the idea of period doubling. However, the idea here is more general and relates to waves that may not be harmonics of one another.
Within stratified layers (in z), Sutherland calculates that the triad of waves will arrange as a cross-hatched pattern as shown in FIG 1 below.
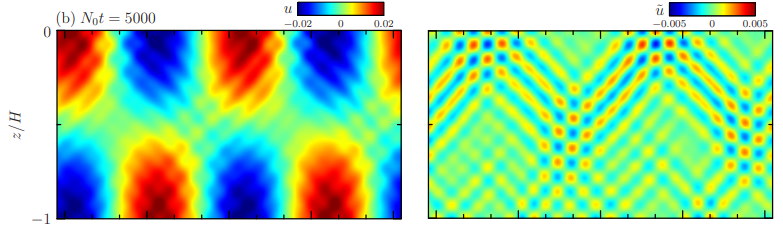
mode-filtered horizontal velocity (right) from a simulation via ref [2]
This is remarkably similar to what one would expect from the Laplace Tidal Equation (LTE) solution that we developed in Chapter 12 (and in a more detailed fashion than that described in a blog post from last year). A triad-specific LTE solution is shown in FIG 2 below.

The fundamental K is 5 while the child siblings are 50 & 45.
The cross-hatching pattern along the stratification layers is straightforwardly generated from a triad of LTE modulation terms (see FIG 3) with a linear phase shift with respect to the stratification layer depth z. That’s at a snapshot in time so the entire contour will also pulsate over time according to the tidal forcing applied.

Next, FIG 4 shows with the tidal forcing applied and an LTE modulation as shown in the upper inset (compare the inset to FIG 3) . In each case, the LTE modulation is not uniform over the fundamental period but the beat period matches the fundamental.

Sutherland has other recent papers [1][3][4] with some discussion on how superharmonics form in [3] .

As noted in a previous blog post, this cascade amplification closer to the equator may help explain why the LTE wave solution aligned precisely along the equator sustains a standing wave mode with characteristic Mach-Zehnder superharmonics. (Note: Terms such as “sibling waves” and “superharmonic cascade” that Sutherland has coined don’t have many search hits, so this appears to be a new overall approach)
As any agreement with the complete x-z-time representation requires a full accounting of the tidal forcing, Sutherland and his colleagues need to pursue this path to further validate their ideas. Matching to the empirical data as I have demonstrated here is a first step.
See also discussion at Real Climate about the double-ITCZ problem, which came up right before this revelation and may have some relevance.
References
- Sutherland, B. R. Internal Waves in the Atmosphere and Ocean: Instability Mechanisms. in Fluid Mechanics of Planets and Stars (eds. Le Bars, M. & Lecoanet, D.) vol. 595 71–89 (Springer International Publishing, 2020).
- Sutherland, B. R. & Jefferson, R. Triad resonant instability of horizontally periodic internal modes. Phys. Rev. Fluids 5, 034801 (2020).
- Baker, L. E. & Sutherland, B. R. The evolution of superharmonics excited by internal tides in non-uniform stratification. Journal of Fluid Mechanics 891, (2020).
- Sutherland, B. R., Achatz, U., Caulfield, C. P. & Klymak, J. M. Recent progress in modeling imbalance in the atmosphere and ocean. Phys. Rev. Fluids4, 010501 (2019)..
- Rajchenbach, J., & Clamond, D. (2015). Faraday waves: Their dispersion relation, nature of bifurcation and wavenumber selection revisited. Journal of Fluid Mechanics, 777, R2.
From reference [4], this schematic
LikeLike
Alpha input
https://www.wolframalpha.com/input/?i=plot+sin%285*x%29*sin%285*sin%28z%29%2Bz%29%2B.4*sin%2850*x%29*sin%2850*sin%28z%29%2Bz%29%2B.1*sin%2845*x%29*sin%2845*sin%28z%29%2Bz%29+for+x%3D-1.2+to+1.2%2C+z%3D-0.5+to+0.5
LikeLike
Pingback: EGU 2020 Notes | GeoEnergy Math
At the EGU, much discussion about triad waves and something struck me that should be obvious, related to ENSO
https://meetingorganizer.copernicus.org/EGU2020/EGU2020-18419.html
“Experimental internal gravity wave turbulence”
I commented:
The triad comes about from the annual impulse modulating the tidal forcing, creating the mirrored DSSC modulated spectrum, see this post
https://geoenergymath.com/2019/10/24/autocorrelation-in-power-spectra-continued/
BTW, this is the higher harmonic mirrored set, at frequencies between 1 and 2 per year
LikeLike
Pingback: Double-Sideband Suppressed-Carrier Modulation vs Triad | GeoEnergy Math