In Chapter 12, we concentrated on the Pacific ocean dipole referred to as ENSO (El Nino/Southern Oscillation).  A dipole that shares some of the characteristics of ENSO is the neighboring Indian Ocean Dipole and its gradient measure the Dipole Mode Index.

The IOD is important because it is correlated with India subcontinent monsoons. It also shows a correlation to ENSO, which is quite apparent by comparing specific peak positions, with a correlation coefficient of 0.2.  This post will describe the differences found via perturbing the ENSO model …

As a starting rationale for explaining why the correlation isn’t higher, there is likely another standing wave solution that complements the major standing wave that stretches across the equatorial Pacific. The latter contributes the majority of ENSO but only a portion of IOD, so the mystery standing wave is what generates the busier cyclic behavior of IOD.

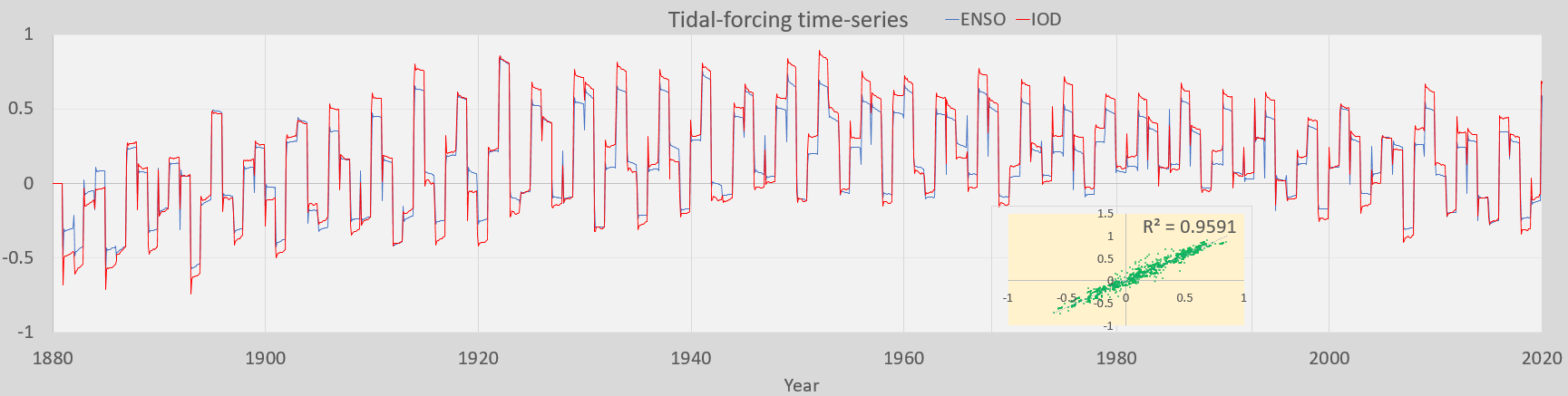
As with the other oceanic indices, the IOD model generates a similar tidal forcing to ENSO, with R^2>0.95.

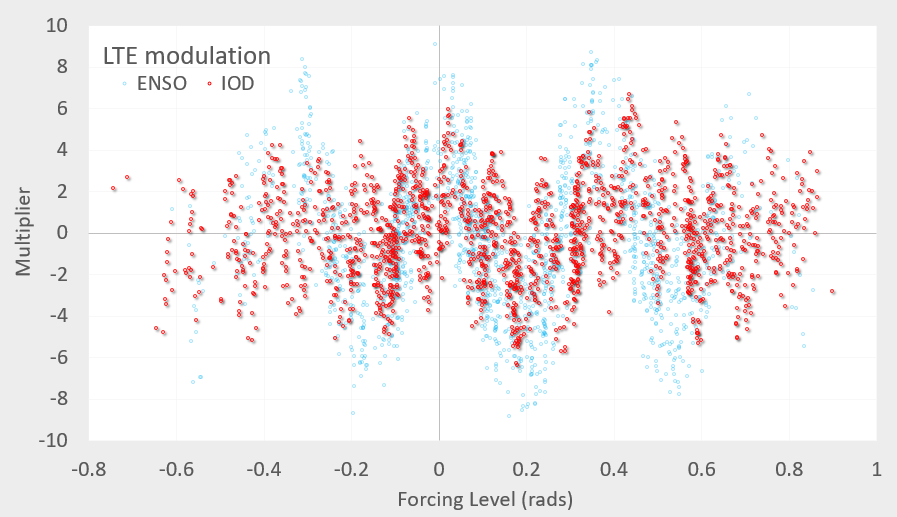
What differs from the ENSO model is the Laplace’s Tidal Equation (LTE) modulation — the IOD consists of a LTE background similar to ENSO, but also a faster modulation that is 3 to 4 that of the background. This can be seen in Fig 2 below.

The LTE modulation is applied to the tidal forcing during the model fitting process. The fit over the entire time span is good, with the Fourier spectrum in the lower panel of Fig 3 below.

Each of ENSO, PDO, AMO [1], and now IOD have a nearly identical set of fundamental forced tidal cycles but distinct standing mode modulations. The QBO is the only completely atmospheric behavior, and it has a distinct tidal forcing (mainly draconic as opposed to tropical for the oceanic indices). The NAO model has the semiannual forcing of QBO but the same tidal forcing as ENSO, PDO, AMO, and IOD.

[1] “Ephemeris calibration of Laplace’s tidal equation model for ENSO“, 2018 AGU Fall Meeting. Note: PDO, AMO, and NAO models were evaluated and compared to ENSO but this was too late for inclusion in the book