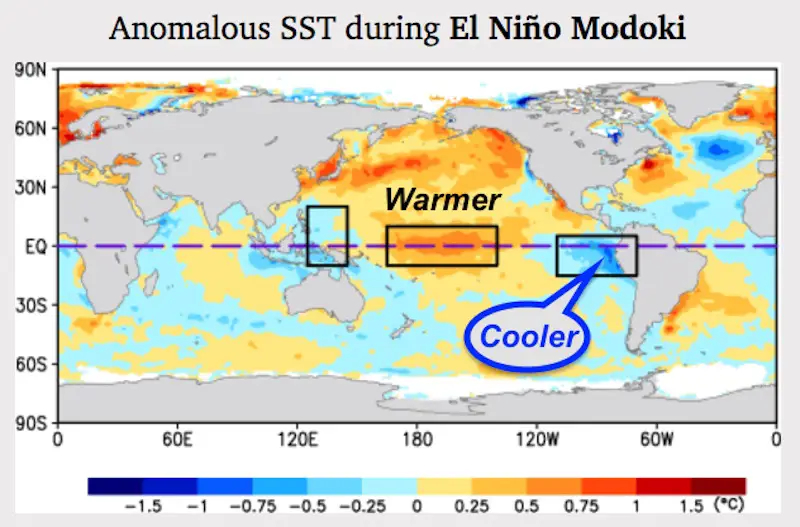
In Chapter 12 of the book we model — via LTE — the canonical El Nino Southern Oscillation (ENSO) behavior, fitting to closely-correlated indices such as NINO3.4 and SOI. Another El Nino index was identified circa 2007 that is not closely correlated to the well-known ENSO indices. This index, referred to as El Nino Modoki, appears to have more of a Pacific Ocean centered dipole shape with a bulge flanked by two wing lobes, cycling again as an erratic standing-wave.
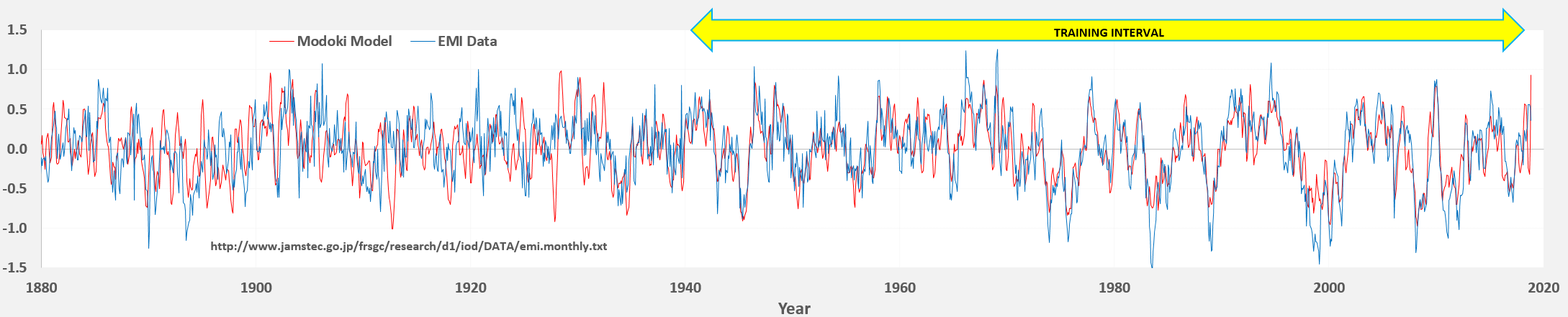
If in fact Modoki differs from the conventional ENSO only by a different standing-wave wavenumber configuration, then it should be straightforward to model as an LTE variation of ENSO. The figure below is the model fitted to the El Nino Modoki Index (EMI) (data from JAMSTEC). The cross-validation is included as values post-1940 were used in the training with values prior to this used as a validation test.
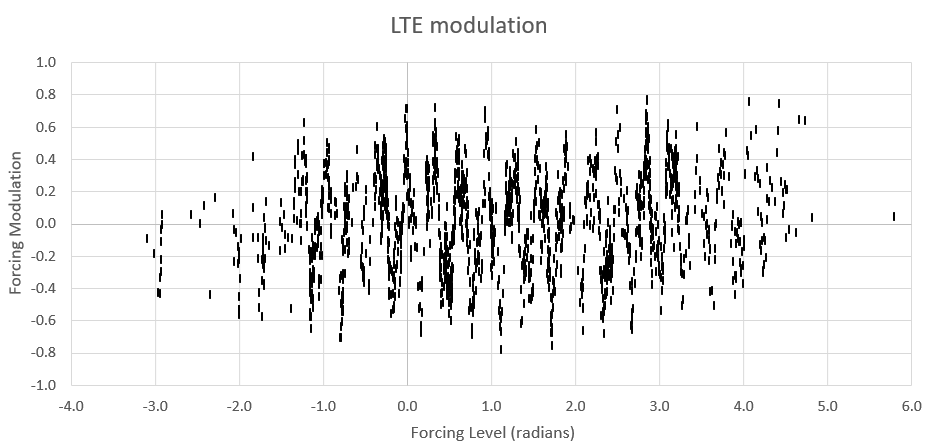
The LTE modulation has a higher fundamental wavenumber component than ENSO (plus a weaker factor closer to a zero wavenumber, i.e. some limited LTE modulation as is found with the QBO model).
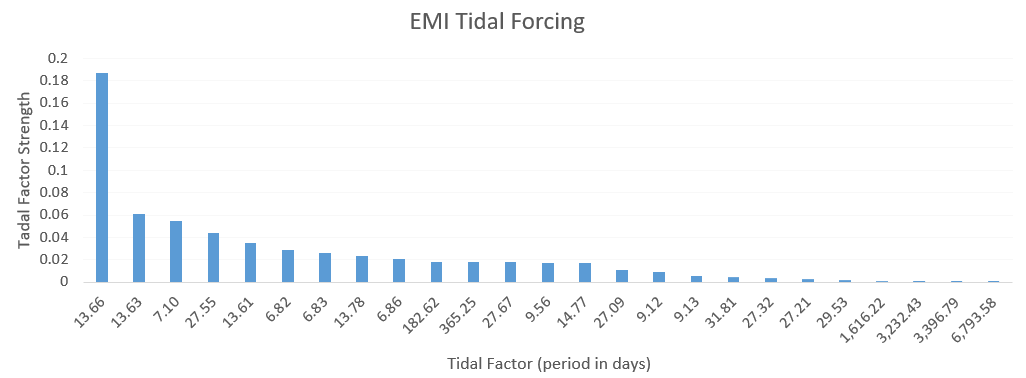
The input tidal forcing is close to that used for ENSO but appears to lead it by one year. The same strength ordering of tidal factors occurs, but with the next higher harmonic (7-day) of the tropical fortnightly 13.66 day tide slightly higher for EMI than ENSO.

The model fit is essentially a perturbation of ENSO so did not take long to optimize based on the Laplace’s Tidal Equation modeling software. I was provoked to run the optimization after finding a paper yesterday on using machine learning to model El Nino Modoki [1].
It’s clear that what needs to be done is a complete spatio-temporal model fit across the equatorial Pacific, which will be amazing as it will account for the complete mix of spatial standing-wave modes. Maybe in a couple of years the climate science establishment will catch up.
References
[1] Pal, Manali, et al. “Long-Lead Prediction of ENSO Modoki Index Using Machine Learning Algorithms.” Scientific Reports, vol. 10, 2020, doi:10.1038/s41598-019-57183-3.
This is the annual impulse of ENSO. Finally it’s been identified.
“New Indices for Better Understanding ENSO by Incorporating Convection Sensitivity to Sea Surface Temperature” https://journals.ametsoc.org/jcli/article/33/16/7045/348273/New-Indices-for-Better-Understanding-ENSO-by
“Because of the seasonally varying SST and EOT, FACT contains the influence from the seasonality of SST, implying a nonlinear interaction between ENSO and seasonal cycle (e.g., Stuecker et al. 2013). ”
What I use as an an input forcing to the ENSO model is the tidal-reinforced annual impulse , which aligns with the longitudinal extent of the Pacific warm pool
After the LTE modulation is applied, then the ENSO cycles are reproduced. This longitudal extent may be the key missing ingredient that the mathematical model required as an intermediate stage of computation. The longitudinal extent thus acts as a lever arm as the erratic tidal-thermocline torque is applied. And the nonlinear LTE modulation does the rest, in terms of creating the standing wave modes necessary to match the Pacific-wide physical behavior.
LikeLiked by 1 person
The ENSO vs Modoki amplitude spectrum of the tidal forcing. Note how the amplitude reverses, which is likely the result of something as innocuous as defining the index in the opposite direction — very similar to SOI versus NINO3.4 which are anti-correlated only because someone long ago decided to define SOI to be opposite of NINO3.4
LikeLiked by 1 person
This is how the Modoki index filters out the main ENSO dipole, revealing mostly the tripole
LikeLiked by 1 person
This comment was noted in the post “what needs to be done is a complete spatio-temporal model fit across the equatorial Pacific”
Now this paper appears in arXiv on July 23: “A Novel Framework for Spatio-Temporal Prediction of Climate Data Using Deep Learning” https://arxiv.org/abs/2007.11836
LikeLiked by 1 person